【第02讲】初等模型 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Python3.11
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案为非完整版教案，请结合课程PPT使用。

最后更新：2024年3月2日

---

2.1 双层玻璃窗的功效

1. 求解双层玻璃建模（符号计算）

import sympy

# 1. 参数定义
# 1.1 定义变量  
Q1, Ta, Tb = sympy.symbols('Q1 Ta Tb')  
# 1.2 定义已知参数（保持为符号）  
k1, k2, T1, T2, d, l = sympy.symbols('k1 k2 T1 T2 d l')  

# 2. 建立方程组  
equ1 = sympy.Eq(Q1, k1 * (T1 - Ta) / d)  
equ2 = sympy.Eq(Q1, k2 * (Ta - Tb) / l)  
equ3 = sympy.Eq(Q1, k1 * (Tb - T2) / d)  

# 3. 使用solve解方程组  
solutions = sympy.solve((equ1, equ2, equ3), (Q1, Ta, Tb), dict=True)
print('Q1 =')
# solutions[0][Q1]
sympy.simplify(solutions[0][Q1])

$Q1 = \frac{k_1 k_2(T_1 - T_2)}{2dk_2 + k_1 l}$

2. 数值可视化分析

通过数值可视化计算（空气厚度与玻璃厚度之比）来分析双层玻璃窗的性能。

import numpy as np
h = np.arange(1,10)        # 定义区间变量 h
r = lambda h: 1 /(1+8*h)   # 定义一个匿名函数接受区间变量 h
print(1 - r(h))

[0.88888889 0.94117647 0.96 0.96969697 0.97560976 0.97959184  0.98245614 0.98461538 0.98630137]

3. 图形可视化

借助图形展示，将变量间的关系可视化，更加直观，便于选择h。

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体  

h = np.arange(1, 100, 0.01)                   # 定义区间变量 h
r = lambda h: 1 /(1+8*h)                      # 定义一个匿名函数接受区间变量 h
y = r(h)

plt.figure(figsize=(5, 3))
plt.plot(h, y, 'r-')                          # 绘图，红色实线
plt.grid(True)                                # 添加网格线
plt.xlabel('1-h(l/d)'), plt.ylabel('Q1/Q2')   # 设置坐标轴标签
plt.title('热量损失比Q2/Q1与h的关系')           # 设置图形标题

Text(0.5, 1.0, '热量损失比Q2/Q1与h的关系')

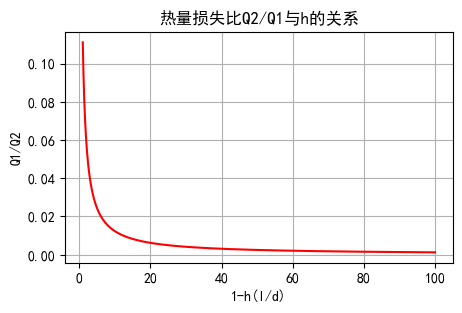
4. 根据效果基本不再改进的方法选择$h$

比如认为 $\frac{|\Delta r|}{|\Delta h|} < 10^{−2}$ 时，两种玻璃在多种环境的影响下，热量损失基本一致。此时，$h$ 每增大 $\Delta h$，r 减小不超过 $10^{−2} |\Delta h|$。若取 $|\Delta h = 0.01|$，则 $r$ 可以通过函数的梯度计算获得。

import numpy as np

df = np.gradient(y, 0.01);      # 计算数值一阶导
n = np.sum(np.abs(df) > 0.01);  # 找到临界位置
h0 = h[n]                       # 临界h值
print('h0 = {:.4f}, r(h0) = {:.4f}'.format(h0, r(h0)))

h0 = 3.4200, r(h0) = 0.0353