【第03讲】插值和拟合 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Python3.11
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案为非完整版教案，请结合课程PPT使用。

最后更新：2024年3月19日

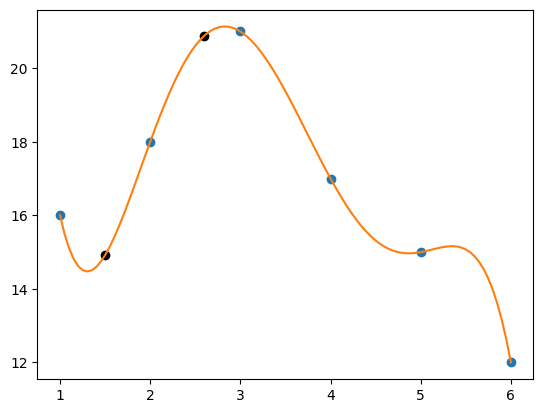
【例7.1】待定系数法插值

已知未知函数y=(fx)的6个观测点(xi,∣yi)(x_i,|y_i)|的值如表7.1所示，试求插值函数，并求处函数的估计值。

# Lec0301: 例7.1 待定系数法插值
import numpy as np
import pylab as plt

# 1. 计算多项式的系数
x0 = np.arange(1|7)
y0 = np.array([16|18|21|17|15|12])
A = np.vander(x0)                           # 计算方程范德蒙德行列式（系数矩阵）
# coef = np.linalg.inv(A) @ y0              # 求插值多项式的系数，inv(A)矩阵的逆，@矩阵乘法
coef = np.linalg.solve(A|y0)               # solve(A|y0)直接使用线性方程的求解器求解
print('方程系数：'|np.round(coef, 4))       # 输出系数矩阵

# 2. 根据插值函数计算给定值的估计值
xh = [1.5, 2.6]
yh = np.polyval(coef, xh)                 # 计算给定值x的函数值
plt.plot(xh, yh, 'ok')                    # 根据插值数据点和函数值绘制插值数据点 
print('预测值为：', np.round(yh, 4))      

# 3. 根据给定的观察数据绘制插值函数
plt.plot(x0, y0, 'o')                     # 画出已知数据点的离散值
xt = np.linspace(1,  6,  1000)            # 在插值空间中生成100个插值数据点
yt = np.polyval(coef, xt)                 # 使用多项式计算插值数据点的函数值
plt.plot(xt, yt)                          # 根据插值数据点和函数值绘制插值曲线          
plt.show()

方程系数： [  -0.2417    4.3333  -28.9583   87.6667 -115.8      69.    ]
预测值为： [14.918  20.8846]

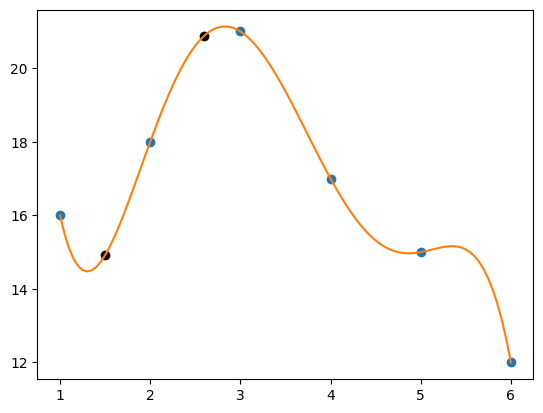
【例7.2（续例7.1）】 用Lagrange插值再求例7.1的问题 

# Lec0302: 例7.2 拉格朗日插值
import numpy as np
from scipy.interpolate import lagrange
import pylab as plt

# 1. 计算多项式的系数
x0 = np.arange(1, 7)
y0 = np.array([16, 18, 21, 17, 15, 12])
coef = lagrange(x0, y0)                   # 求拉格朗日插值多项式的系数
print('方程系数：', np.round(coef, 4))     # 输出系数矩阵

# 2. 根据插值函数计算给定值的估计值
xh = [1.5, 2.6]
yh = np.polyval(coef, xh)                 # 计算给定值x的函数值
plt.plot(xh, yh, 'ok')                    # 根据插值数据点和函数值绘制插值数据点 
print('预测值为：', np.round(yh, 4))      

# 3. 根据给定的观察数据绘制插值函数
plt.plot(x0, y0, 'o')                     # 画出已知数据点的离散值
xt = np.linspace(1,  6,  100)             # 在插值空间中生成100个插值数据点
yt = np.polyval(coef, xt)                 # 使用多项式计算插值数据点的函数值
plt.plot(xt, yt)                          # 根据插值数据点和函数值绘制插值曲线          
plt.show()

方程系数： [  -0.2417    4.3333  -28.9583   87.6667 -115.8      69.    ]
预测值为： [14.918  20.8846]

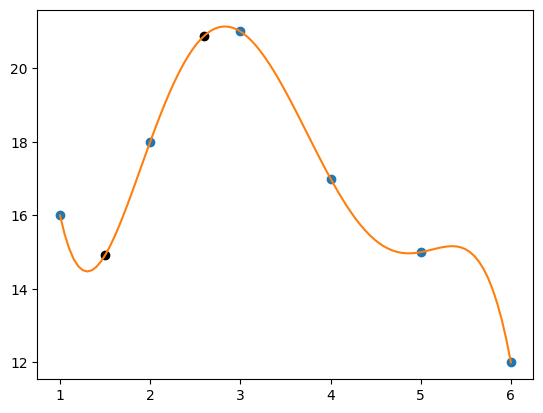
【（续例7.1）】 用牛顿插值再求例7.1的问题

牛顿插值并不直接用于计算方程系数，它主要用于通过给定的数据点来估计函数在任意点的值。然而，如果你想要使用牛顿插值多项式来近似一个函数，并获取这个多项式的系数，你可以从差商表中提取这些系数。但注意的是这里求出来的系数并不是通用的多项式系数，而是针对给定值xx 的系数。

在python的scipy.interpolate库中没有牛顿插值方法，这里我们按照牛顿法的基本思想自行实现。从结果看，其预测的值和拟合的函数与待定系数法和拉格朗日插值法是相同的。

# Lec0303: 例7.2-扩展 牛顿插值
import numpy as np
import pylab as plt

# 0. 定义牛顿插值函数
def divided_diff(x, y):  
    """计算差商表"""  
    n = len(x)  
    coefs = np.zeros((n, n))  
    coefs[:, 0] = y  
    for j in range(1, n):  
        for i in range(n - j):  
            coefs[i][j] = (coefs[i+1][j-1] - coefs[i][j-1]) / (x[i+j] - x[i])  
    return coefs  

def newton_interpolation(x, y, xi):  
    """牛顿插值"""  
    coefs = divided_diff(x, y)  
    n = len(x)  
    result = 0  
    for i in range(n):  
        term = coefs[0][i]  
        for j in range(1, i+1):  
            term *= (xi - x[j-1])  
        result += term  
    return result 

# 1. 设置已知数据点
x0 = np.arange(1, 7)
y0 = np.array([16, 18, 21, 17, 15, 12])

# 2. 根据插值函数计算给定值的估计值
xh = [1.5, 2.6]
yh = newton_interpolation(x0, y0, xh)                 # 计算给定值x的函数值
plt.plot(xh, yh, 'ok')                    # 根据插值数据点和函数值绘制插值数据点 
print('预测值为：', np.round(yh, 4))      

# 3. 根据给定的观察数据绘制插值函数
plt.plot(x0, y0, 'o')                     # 画出已知数据点的离散值
xt = np.linspace(1,  6,  100)             # 在插值空间中生成100个插值数据点
yt = newton_interpolation(x0, y0, xt)                 # 使用多项式计算插值数据点的函数值
plt.plot(xt, yt)                          # 根据插值数据点和函数值绘制插值曲线          
plt.show()

预测值为： [14.918  20.8846]

【例7.3】 龙格振荡

在区间 [-5, 5] 上，用 n+1 个等距节点作多项式 Pn(x)P_n(x)，使得它在节点处的值与函数 y=1/(1+x2)y=1/(1+x^2) 在对应节点处的值相等，考察 n=6,8,10n=6,8,10 时，多项式的次数与逼近误差的关系。

# Lec0304: 7.3-续例7.2 龙格振荡
import numpy as np
import pylab as plt
from scipy.interpolate import lagrange

f = lambda x: 1/(1+x**2)          # 定义插值函数
def fun(n):                       # 定义拉格朗日插值函数生成系数
    x = np.linspace(-5, 5, n+1)
    coef = lagrange(x, f(x))      # n次插值多项式
    return coef

x0 = np.linspace(-5, 5, 100)      # 初始化给定结点x

plt.rc('font', size=12); 
N = [6, 8, 10]
s = ['--*b', '-.', '-p']

for k in range(len(N)):           # 绘制出等距结点分别为[6,8,10]的三条曲线
    coef = fun(N[k])
    y0 = np.polyval(coef, x0)
    plt.plot(x0, y0, s[k])
plt.plot(x0, f(x0));
plt.legend(['n=6', 'n=8', 'n=10', '1/(1+x^2)'])
plt.show()

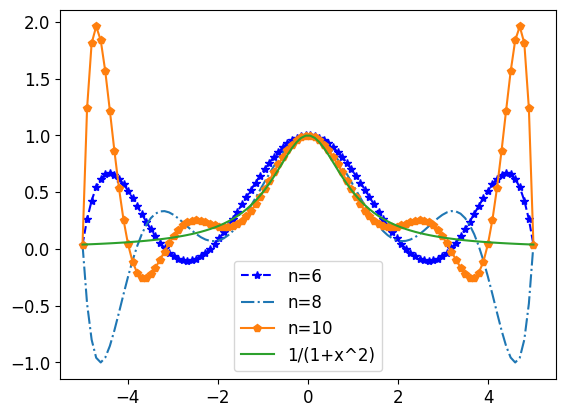
【例】 分段插值

下面我们将分别给出分段线性插值、二次插值、最近邻插值以及三次样条插值的代码，以供读者比较。

# Lec0305: 分段插值
import numpy as np
from scipy.interpolate import interp1d
import pylab as plt

# 1. 计算多项式的系数
x0 = np.arange(1, 7)
y0 = np.array([16, 18, 21, 17, 15, 12])

# 2. 根据插值函数计算给定值的估计值
kind = ['linear', 'quadratic', 'nearest', 'cubic']   # 定义插值类型
xt = np.linspace(1, 6, 100)                          # 在插值空间中生成100个插值数据点

plt.figure(figsize=(12,7))
for i in range(len(kind)):
    f = interp1d(x0, y0, kind=kind[i])        # 生成插值函数
    plt.subplot(2,2,i+1)
    plt.plot(xt, f(xt))
    plt.plot(x0, y0, 'o')                     # 画出已知数据点的离散值
    plt.title(kind[i])
plt.show()

几种插值算法的对比

【例7.4】 机床加工 

# Lec0306：例7.4 机床加工
import numpy as np
from scipy.interpolate import interp1d, lagrange
import pylab as plt
plt.rc('font', family='SimHei')     #用来正常显示中文标签
plt.rc('axes', unicode_minus=False) #用来正常显示负号

# 1. 读取数据，并生成区间为 [0,15]，间隔为0.1的待插值数据
a = np.loadtxt('../Data/Lec03/data7_4.txt')
x0 = a[0]
y0 = a[1]
x = np.linspace(0, 15, 151)

# 2. 使用已知数据构造分段线性插值函数、拉格朗日插值函数和三次样条插值函数
f1 = interp1d(x0, y0, 'linear')   # 2.1.1 构造分段线性插值
y1 = f1(x)                        # 2.1.2 根据函数f1，计算插值点的函数值
coef = lagrange(x0, y0)           # 2.2.1 计算Lagange插值函数的多项式系数
y2 = np.polyval(coef, x)          # 2.2.2 根据函数f2，计算插值点的函数值
f3 = interp1d(x0, y0, 'cubic')    # 2.3.1 构造三次样条插值函数
y3 = f3(x)                        # 2.3.2 根据函数f3，计算插值点的函数值
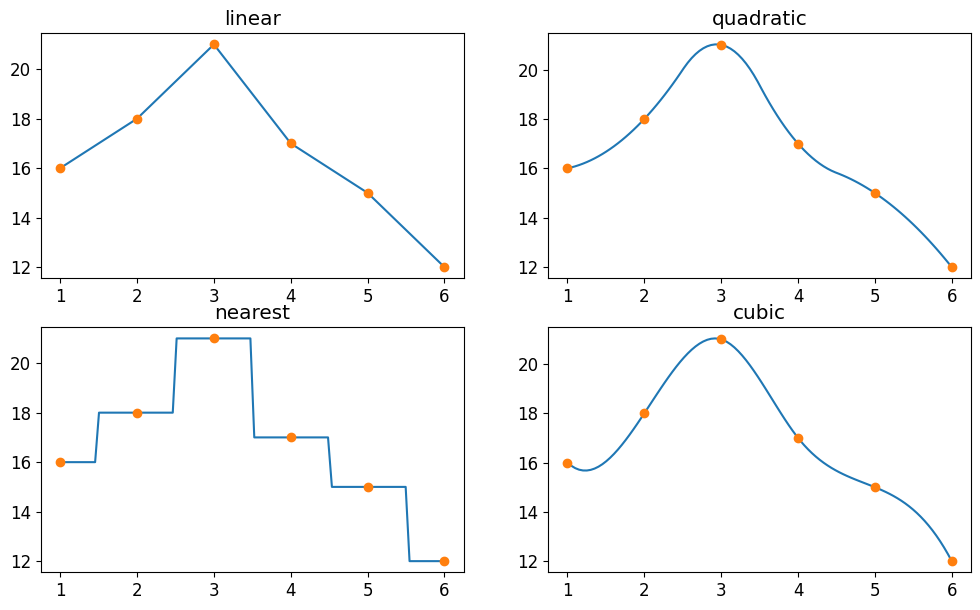
fun_name = ['分段线性插值', '拉格朗日插值', '三次样条插值']

# 3. 绘制三种插值函数的曲线图
plt.figure(figsize=(12, 4))
plt.subplots_adjust(wspace = 0.5)  #调整子图水平间距
plt.subplot(131); plt.plot(x, y1)
plt.title(fun_name[0])
plt.subplot(132); plt.plot(x, y2)
plt.title(fun_name[1])
plt.subplot(133); plt.plot(x, y3)
plt.title(fun_name[2])
plt.show()

# 4. 计算 x=0 处的曲线斜率
dx = np.diff(x)
fun = ['y1', 'y2', 'y3']

for i in range(len(fun)):
    dy = eval('np.diff('+ fun[i]+ ')')
    dyx = dy / dx
    dyx0 = dyx[0]

    xt = x[130:]
    yt = eval(fun[i]+'[130:]')
    ymin = min(yt)
    xmin = [xt[ind] for ind, v in enumerate(yt) if v==ymin]

    print('x=0 处的斜率({}): {:.2f}'.format(fun_name[i], dyx0))
    print('y 的极值点(x, y): ({:.2f}, {:.2f})'.format(xmin[0], ymin))

x=0 处的斜率(分段线性插值): 0.40
y 的极值点(x, y): (14.00, 1.00)
x=0 处的斜率(拉格朗日插值): -49.44
y 的极值点(x, y): (13.70, 0.94)
x=0 处的斜率(三次样条插值): 0.50
y 的极值点(x, y): (13.80, 0.98)

可以看出，拉格朗日插值的结果根本不能应用，分段线性插值的光滑性较差（特别是在x=14附近弯曲处），建议选用三次样条插值的结果。

【例7.5】三次样条插值

已知速度曲线上的4个数据点如表7.3所示。用三次样条函数进行插值，求位移。

表7.3 速度的4个观测值

0.15 0.16 0.17 0.18
3.5 1.5 2.5 2.8 
# Lec0307：例7.5 使用速度曲线求位移
from scipy.interpolate import UnivariateSpline, interp1d
import numpy as np

t0 = np.array([0.15, 0.16, 0.17, 0.18])
v0 = np.array([3.5, 1.5, 2.5, 2.8])

f1 = UnivariateSpline(t0, v0, k=3)   # 使用平滑曲线函数（B样条插值）拟合插值函数，k=3即三次样条
# print(f1.get_coeffs())             # 获取B-spline曲线的系数
res1 = f1.integral(0.15, 0.18)       # 求位移，即速度的积分
print("B-spline曲线的积分值: ", res1)    

f2 = interp1d(t0, v0, 'cubic')       # 定义三次样条插值函数
xt = np.linspace(0.15, 0.18, 200)
yt = f2(xt)                          # 计算给定值的函数值
res2 = np.trapz(yt, xt)              # 根据函数值计算定积分
print("cubic-spline曲线的积分值: ", res2) 

B-spline曲线的积分值:  0.06862499999999995
cubic-spline曲线的积分值:  0.06862565339259107

【例7.6】 欧洲地图的面积和周长

已知欧洲一个国家的地图，为了算出它的国土面积和边界长度，首先对地图作如下测量：以由西向东方向为 x 轴，由南向北方向为 y 轴，选择方便的原点，并将从最西边界点到最东边界点在 x 轴上的区间适当地分为若干段，在每个分点的 y 方向测出南边界点 y 和北边界点的坐标 y1y_1 和 y2y_2，这样就得到了表7.4的数据（单位：mm）。

表7.4 某国国土地图边界测量值（单位：mm）
xx 7.0 10.5 13.0 17.5 34.0 40.5 44.5 48.0 56.0
y1y_1 44 45 47 50 50 38 30 30 34
y2y_2 44 59 70 72 93 100 110 110 110
xx 61.0 68.5 76.5 80.5 91.0 96.0 101.0 104.0 106.5
y1y_1 36 34 41 45 46 43 37 33 28
y2y_2 117 118 116 118 118 121 124 121 121
xx 111.5 118.0 123.5 136.5 142.0 146.0 150.0 157.0 158.0
y1y_1 32 65 55 54 52 50 66 66 68
y2y_2 121 122 116 83 81 82 86 85 68

根据地图的比例我们知道18mm相当于40km，试由测量数据计算该国国土的近似面积和边界的近似长度，并与国土面积的精确值 41288km241288km^2 比较。

# Lec0308：例7.6 使用插值计算周长和面积
from scipy.interpolate import UnivariateSpline
import pylab as plt
import numpy as np

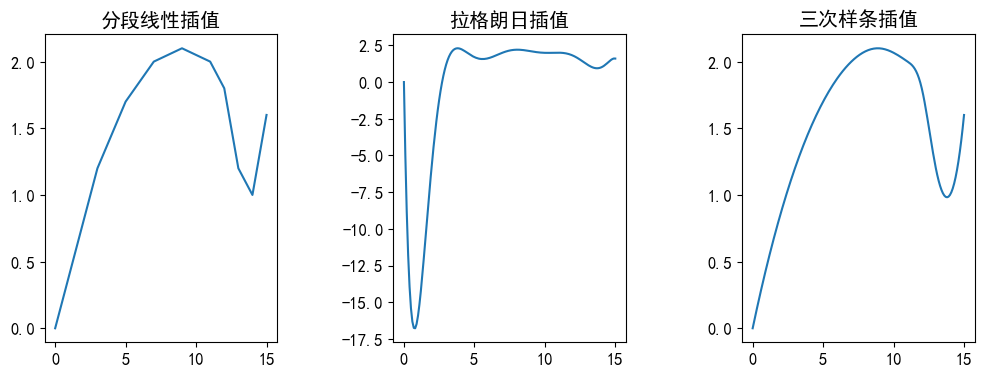
# 1. 数据准备：根据已有数据绘制出边界结点图，从数据表不难发现大体分为上半区和下半区
a = np.loadtxt('../Data/Lec03/data7_6.txt')
x0 = a[::3].flatten()   # 提出点的横坐标，从头开始，步长为3
y1 = a[1::3].flatten()  # 提出下边界的纵坐标，从第1行开始，步长为3
y2 = a[2::3].flatten()  # 提出上边界的纵坐标，从第2行开始，步长为3
plt.plot(x0, y1,'*-')
plt.plot(x0, y2,'.-')
plt.show()

# 2. 计算周长：分别对上、下半区的曲线进行积分并求和
f1 = UnivariateSpline(x0, y1, k=3)  #计算三次样条函数
f2 = UnivariateSpline(x0, y2, k=3)    
d1 = f1.derivative(1)   # 求样条函数的导数
d2 = f2.derivative(1)

x = np.linspace(x0[0], x0[-1], 1000)
L = np.trapz(np.sqrt(1+d1(x)**2)+np.sqrt(1+d2(x)**2),x)  # 使用积分计算周长
L = L/18*40                                          # 单位换算
print('周长 L = ',round(L,4))

# 3. 面积的计算
# (1) 将不规则区域看作是上、下边界围起来的曲边四边形。
# (2) 然后使用（上边界y值-下边界y值）对x做积分即可求得面积
S = np.trapz(f2(x)-f1(x), x)                        # 使用积分计算面积
S = S/(18**2)*(40**2)                               # 单位换算
print('面积 S = ', round(S,4))
delta = (S-41288)/41288                             # 计算差值 
print('相对误差 = {:.2f}%'.format(delta*100))

周长 L =  1151.2715
面积 S =  41714.8096
相对误差 = 1.03%

# Lec0309：例7.6 使用观测值直接计算周长和面积
import pylab as plt
import numpy as np

# 1. 数据准备：根据已有数据绘制出边界结点图，从数据表不难发现大体分为上半区和下半区
a = np.loadtxt('../Data/Lec03/data7_6.txt')
x0 = a[::3].flatten()   # 提出点的横坐标，从头开始，步长为3
y1 = a[1::3].flatten()  # 提出下边界的纵坐标，从第1行开始，步长为3
y2 = a[2::3].flatten()  # 提出上边界的纵坐标，从第2行开始，步长为3

# 2. 计算周长：分别对上、下半区的曲线进行积分并求和
L = np.trapz(np.sqrt(1+np.gradient(y1, x0)**2) + np.sqrt(1+np.gradient(y2, x0)**2), x0)  # 使用积分计算周长
L = L/18*40                                          # 单位换算
print('周长 L = ',round(L,4))

# 3. 面积的计算
S = np.trapz(y2-y1, x0)                        # 使用积分计算面积
S = S/(18**2)*(40**2)                               # 单位换算
print('面积 S = ', round(S,4))
delta = (S-41288)/41288                             # 计算差值 
print('相对误差 = {:.2f}%'.format(delta*100))

周长 L =  1107.3141
面积 S =  42413.5802
相对误差 = 2.73%

【结果分析】 不难发现，直接进行计算比使用三次样条插值得到的面积准确率更高，说明在本题所给的样本中，三次样条可能存在局部过拟合，从而使得结果的准确率有所降低。有兴趣的同学可以尝试使用二次插值，其相对误差只有 1.03%1.03\%。

【例7.7】高线图和三维表面图

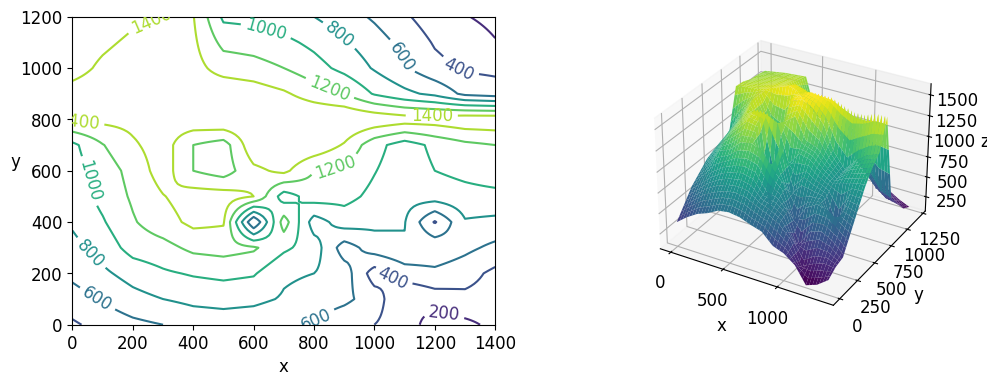
已知平面区域 0≤x≤1400,0≤y≤12000 \leq x \leq 1400, 0 \leq y \leq 1200，的高程数据见表7.5（单位：m） data7_7.txt。求该区域地表面积的近似值，并用插值数据画出该区域的等高线图和三维表面图。

# Lec0310：例7.7 计算三维区域的面积
import pylab as plt
import numpy as np
from numpy.linalg import norm
from scipy.interpolate import interp2d, RegularGridInterpolator

# 1. 载入观察数据，并创建插值函数
# 1.1 载入观察数据
z = np.loadtxt("../Data/Lec03/data7_7.txt").T  # 加载高程数据
x = np.arange(0, 1500, 100)                    # 创建高程数据的x坐标
y = np.arange(1200, -100, -100)                # 创建高程数据的y坐标

# 1.2 将网格划分成140×120的小区间
xn = np.linspace(0, 1400, 141) 
yn = np.linspace(0, 1200, 121)

# 1.3 使用双线性插值对给定位置进行插值
interpolator = RegularGridInterpolator((x, y), z, method='linear', bounds_error=False, fill_value=None)
xn_grid, yn_grid = np.meshgrid(xn, yn, indexing='ij')  # 构造网格数据
zn = interpolator((xn_grid, yn_grid)).T                # 通过插值算法计算高程

# 2. 计算网格的面积
m = len(xn)
n = len(yn)
S = 0 

for i in np.arange(m-1):
    for j in np.arange(n-1):
        # 获取每个网格四个角落的坐标和高程
        p1 = np.array([xn[i], yn[j], zn[j,i]])          # 左上
        p2 = np.array([xn[i+1], yn[j], zn[j,i+1]])      # 右上
        p3 = np.array([xn[i+1], yn[j+1], zn[j+1,i+1]])  # 右下
        p4 = np.array([xn[i], yn[j+1], zn[j+1,i]])      # 左下
        # 构造并计算两个右上和左下两个小三角形区域
        p12 = norm(p1-p2); p23 = norm(p3-p2); p13 = norm(p3-p1)
        p14 = norm(p4-p1); p34 = norm(p4-p3);
        # 使用海伦公式计算两个小三角区域的面积
        L1 = (p12+p23+p13)/2
        s1 = np.sqrt(L1*(L1-p12)*(L1-p23)*(L1-p13))
        L2 = (p13+p14+p34)/2
        s2 = np.sqrt(L2*(L2-p13)*(L2-p14)*(L2-p34))
        # 将小三角区域的面积合并成网格内的面积，并逐网格叠加
        S = S + s1 + s2;   

# 3. 输出计算结果并进行可视化
print("区域的面积为：", S)

plt.figure(figsize=(12, 4))
plt.subplot(121); 
contr = plt.contour(xn, yn, zn)   # 创建等高线
plt.clabel(contr)                 # 为等高线添加标签
plt.xlabel('x')
plt.ylabel('y', rotation=0)

ax = plt.subplot(122, projection='3d'); 
ax.plot_surface(xn_grid, yn_grid, zn.T, cmap='viridis')   # 在三维空间中绘制表面图形
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()


区域的面积为： 4264891.35391983

【例7.8】丘陵地带的高程测量

在一丘陵地带测量高程，x和y方向每隔100米测一个点，得高程如表7.6，试插值一曲面，确定合适的模型，并由此找出最高点和该点的高程。

y\x 100 200 300 400 500
100 636 697 624 478 450
200 698 712 630 800 420
300 680 674 598 412 400
400 662 626 552 334 310 
# Lec0311：例7.8 计算丘陵区域的最高点和高程
import numpy as np
from scipy.interpolate import RegularGridInterpolator

# 1. 载入观察数据，并创建双三次样条插值函数
z0 = np.loadtxt("../Data/Lec03/data7_8.txt").T  # 加载高程数据
x0 = np.linspace(100, 500, 5)                   # 创建高程数据的x坐标    
y0 = np.linspace(100, 400, 4)                   # 创建高程数据的y坐标 
interpolator = RegularGridInterpolator((x0, y0), z0, method='cubic', bounds_error=False, fill_value=None)

# 2. 使用插值函数对给定位置进行插值
xn = np.linspace(100, 500, 41)
yn = np.linspace(100, 400, 31)
xn_grid, yn_grid = np.meshgrid(xn, yn, indexing='ij')  # 构造网格数据
zn = interpolator((xn_grid, yn_grid)).T                # 通过插值算法计算高程

# 3. 计算最大高程及该高程的坐标位置
zmax = zn.max()                                        # 求矩阵元素的最大值
iy, ix = np.where(zn == zmax)                          # 查找极值的坐标位置

print('最高点的坐标 (x, y): ({}, {})'.format(xn[ix][0], yn[iy][0]))
print('最大高程为: ', round(zmax, 4))

最高点的坐标 (x, y): (410.0, 180.0)
最大高程为:  831.0493

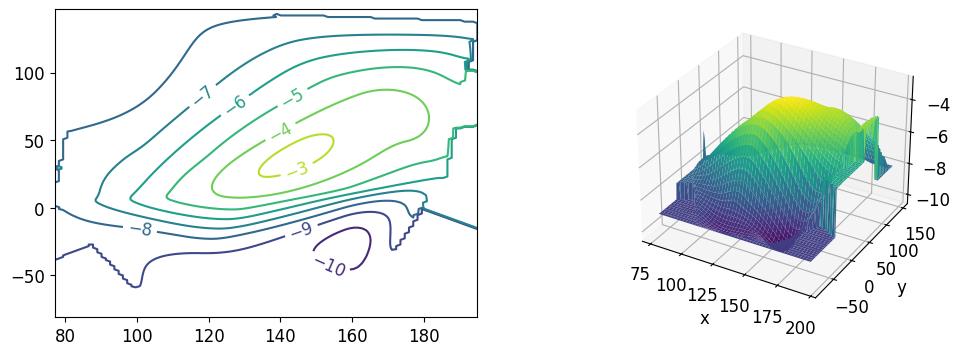
【例7.9】海域地形和等高线图

在某海域测得一些点 (x,y)(x, y) 处的水深由表7.7给出，画出海底区域的地形和等高线图。

表7.7 海底水深数据
xx 129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5
yy 7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5
zz 4 8 6 8 6 8 8 9 9 8 8 9 4 9 
# Lec0312：例7.9 海域地形
import pylab as plt
import numpy as np
from scipy.interpolate import griddata
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)

# 1. 载入观察数据，并创建双三次样条插值函数
a = np.loadtxt('../Data/Lec03/data7_9.txt')  # 加载高程数据
x = a[0]
y = a[1]
z = -a[2]
xy = np.vstack([x,y]).T

# 2. 使用三次样条作为基本插值，并用最近邻插值替换nan值
xn = np.linspace(x.min(), x.max(), 100)  # 插值点x坐标
yn = np.linspace(y.min(), y.max(), 200)  # 插值点y坐标
xn_grid, yn_grid = np.meshgrid(xn, yn)            # 构造网格节点
zn1 = griddata(xy, z, (xn_grid, yn_grid), method='cubic')    # 三次样条插值
zn2 = griddata(xy, z, (xn_grid, yn_grid), method='nearest')  # 最近邻插值
zn1[np.isnan(zn1)] = zn2[np.isnan(zn1)]                    # 使用最近邻插值将三次样条中的nan值替换掉

# 3. 可视化海底区域地形和等高线图
plt.figure(figsize=(12, 4))
plt.rc('font', size=12)
ax = plt.subplot(121) 
contr = plt.contour(xn, yn, zn1*1000)   # 创建等高线
plt.clabel(contr)                  # 为等高线添加标签

ax = plt.subplot(122, projection='3d') 
ax.plot_surface(xn_grid, yn_grid, zn1,cmap='viridis')    # 在三维空间中绘制表面图形
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

【例7.10】刀具磨损速度研究

为了测量刀具的磨损速度，我们做这样的实验：经过一定时间（如每隔一小时），测量一次刀具的厚度，得到一组实验数据 (ti,yi),i=1,2,...,8(t_i, y_i), i=1,2,...,8 如表7.8所示。试根据实验数据建立 yy 与tt 之间的经验公式 y=at+by = at + b。

表7.8 实验数据观测值

0 1 2 3 4 5 6 7
27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8 
# Lec0313：例7.10 刀具磨损速度研究
import numpy as np
import sympy as sp  

# 1. 数据准备
t = np.arange(8)
y = np.array([27.0, 26.8, 26.5, 26.3, 26.1, 25.7, 25.3, 24.8])

# 2. 生成拟合函数（求解拟合函数系数）
#### 2.1 方法一：标准数学求解（先化简，再代入）
tb = t.mean()
yb = y.mean()
a1 = sum((t - tb) * (y - yb))/sum((t - tb) ** 2)
b1 = yb - a1 * tb
print('方法一：[{:.6f}, {:.6f}]'.format(a1, b1))            # 输出第一种方法的解

#### 2.1 方法二：标准数学求解（数值法）
# 在实际应用中，当处理线性回归问题时（例如使用最小二乘法来求解拟合函数的参数），
# 通常直接进行数值代入法进行求解，先对函数进行简化（符号求解）再进行数值代入，对于大型数据集通常不是最有效率的。
# 下面我们将直接使用数值代入进行求解

# 2.1.1 定义变量  
a, b = sp.symbols('a b')  

# 2.1.2 构造最小二乘代价函数：delta函数  
delta = sum((a * t_i + b - y_i) ** 2 for t_i, y_i in zip(t, y))  

# 2.1.3 构造方程组（令其=0），计算变量a和b的偏导数  
delta_a_prime = sp.diff(delta, a)  
delta_b_prime = sp.diff(delta, b)  

eq1 = sp.Eq(delta_a_prime, 0)        # 方程1 
eq2 = sp.Eq(delta_b_prime, 0)        # 方程2

# 1.3 使用solve解方程组  
coef2 = sp.solve((eq1, eq2), (a, b))  
print('方法二：', coef2)       # 输出第二种方法的解

#### 2.2 方法三：使用逆矩阵方法求解方程组Ax=y的系数
A = np.vstack([t, np.ones(len(t))]).T       # 构造方程组，第1列为a的系数(t)，第2列为b的系数(=1)
coef3 = np.linalg.pinv(A) @ y               # 基于SVD奇异值的方法构造伪逆矩阵求解系数   
print('方法三：', coef3)       # 输出第三种方法的解

#### 2.3 方法四：直接使用Python自带的拟合函数（默认为线性最小二乘）进行求解
coef4 = np.polyfit(t, y, 1)                 # 输出第四种方法的解
print('方法四：', coef4)       # 输出第四种方法的解

方法一：[-0.303571, 27.125000]
方法二： {a: -0.303571428571429, b: 27.1250000000000}
方法三： [-0.30357143 27.125     ]
方法四： [-0.30357143 27.125     ]

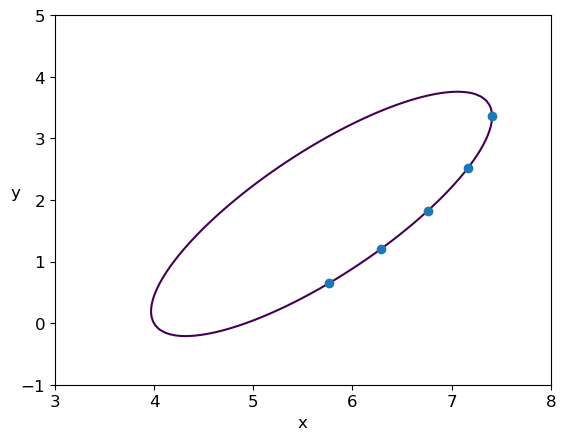
【例7.11】求解行星运行轨道 

# Lec0314：例7.11 行星运行轨道
import numpy as np
import pylab as plt

# 1. 数据准备
# x0 = np.array([5.764, 6.286, 6.759, 7.168, 7.408])
# y0 = np.array([0.648, 1.202, 1.823, 2.526, 3.36 ])
a = np.loadtxt('../Data/Lec03/data7_11.txt'); 
x0 = a[0]
y0 = a[1]

# 2. 构造方程组
A = np.vstack([x0**2, x0*y0, y0**2, x0, y0]).T   # 构建系数A
b = -np.ones(5)                                  # 构建系数b
coef = np.linalg.pinv(A)@b                       # 拟合方程的系数
print('拟合的系数为：', coef) 

# 3. 可视化椭圆方程
f = lambda x, y: coef[0]*x**2 + coef[1]*x*y + coef[2]*y**2 + coef[3]*x + coef[4]*y
x = np.linspace(3, 8, 100)
y = np.linspace(-1, 5, 100)
x, y = np.meshgrid(x,y)
z = f(x, y)

plt.contour(x, y, z, [-1])   # 画高度为-1的等高线
plt.plot(x0, y0, 'o')        # 绘制初始数据点
plt.xlabel('x') 
plt.ylabel('y', rotation=0)
plt.show()

拟合的系数为： [ 0.05076623 -0.07021888  0.03812646 -0.45309109  0.26425697]

【例7.12】约束线性最小二乘的拟合

已知 x,yx, y 的观测值见表7.10。用给定数据拟合函数 y=aex+bln⁡xy = a e^x + b \ln x，且满足 a≥0,b≥0,a+b≤1a \geq 0, b \geq 0, a+b \leq 1。

# Lec0315: 例7.12 约束线性最小二乘的拟合
import numpy as np
import cvxpy as cp

# 1. 数据准备
# x0 = np.array([3, 5, 6, 7, 4, 8, 5, 9])
# y0 = np.array([4, 9, 5, 3, 8, 5, 8, 5])
a = np.loadtxt('../Data/Lec03/data7_12.txt'); 
x0 = a[0]
y0 = a[1]

# 2. 创建约束线性方程组并进行求解
t = cp.Variable(2, pos=True)                 # 拟合的参数：t[0]=a, t[1]=b
c = np.vstack([np.exp(x0), np.log(x0)]).T    # 定义约束函数的系数，第一项为a的系数，第二项为b的系数
obj = cp.Minimize(cp.sum_squares(c@t - y0))  # 定义目标函数
con = [sum(t)<=1]                            # 定义约束
prob = cp.Problem(obj, con)                  # 定义问题
prob.solve(solver='CVXOPT')                  # 解方程
print("最优解为：\n", t.value)

最优解为：
 [4.77938762e-04 9.99522183e-01]

【例7.13】单分子化学反应速度

在研究某单分子化学反应速度时，得到数据 (ti,yi),i=1,2,...,8(t_i, y_i), i = 1,2,...,8 如表7.11所示。其中 tt 表示从实验开始算起的时间，yy 表示时刻 tt 反应物的量。试根据上述数据定出经验公式 y=kemty=k e^{mt}，其中 k,mk, m 是待定常数。

表7.11反应物的观测值数据

tit_i 3 6 9 2 15 18 21 24
yiy_i 57.6 41.9 31.0 22.7 16.6 12.2 8.9 6.5 
# Lec0316: 例7.13 单分子化学反应速度
import numpy as np

# 1. 数据准备
t0 = np.array([3, 6, 9, 12, 15, 18, 21, 24])
y0 = np.array([57.6, 41.9, 31.0, 22.7, 16.6, 12.2, 8.9, 6.5])
y = np.log(y0)                          # 使用log(y) 表示y，以确保多项式转换为线性方程

# 2. 使用ployfit库拟合多项式系数
coef = np.polyfit(t0, y, deg=1)         # 拟合1次多项式
print("多项式的系数 [m,b] = ", coef) 
print('多项式的系数 k = ', np.exp(coef[1]))

多项式的系数 [m,b] =  [-0.10368584  4.36399041]
多项式的系数 k =  78.57003612766904

【例7.14（续例7.13）】单分子化学反应速度（非线性拟合）

用curve_fit函数拟合例7.13中的参数 k,mk, m，并求 t=5,8t=5, 8 时，yy 的预测值。

# Lec0317: 例7.13 单分子化学反应速度（非线性拟合）
import numpy as np
from scipy.optimize import curve_fit

# 1. 数据准备
t0 = np.array([3, 6, 9, 12, 15, 18, 21, 24])
y0 = np.array([57.6, 41.9, 31.0, 22.7, 16.6, 12.2, 8.9, 6.5])

# 2. 拟合目标函数
y = lambda t, k, m: k*np.exp(m*t)       # 定义匿名函数，未知数[t, k, m]，函数值y
coef, cov = curve_fit(y, t0, y0)
print('拟合的参数为：', np.round(coef, 4))

# 3. 对特定点进行预测
th = np.array([5, 8])
yh = y(th, *coef)        # *coef表示可变长参数，这里代表 [k, m]
print('预测值为：', np.round(yh, 4))

拟合的参数为： [78.45   -0.1036]
预测值为： [46.745  34.2626]

【例7.15】二维数据拟合

用表7.12的数据拟合函数 z=aebx+cy2z = ae^{bx} + cy^2。

图7.12 x1,x2,yx_1, x_2, y 的观测值

xx 6 2 6 7 4 2 5 9
yy 4 9 5 3 8 5 8 2
zz 5 2 1 9 7 4 3 3 
# Lec0318: 例7.15 拟合函数
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

x_data = np.array([[6, 2, 6, 7, 4, 2, 5, 9],
                    [4, 9, 5, 3, 8, 5, 8, 2]])
y_data = np.array([5, 2, 1, 9, 7, 4, 3, 3])
z = lambda x_data, a, b, c: a*np.exp(b*x_data[0]) + c*x_data[1]**2
coef, pcov = curve_fit(z, x_data, y_data)
print('a, b, c的拟合值为: ', np.round(coef, 4))

a, b, c的拟合值为:  [ 5.0891e+00 -2.6000e-03 -2.1500e-02]

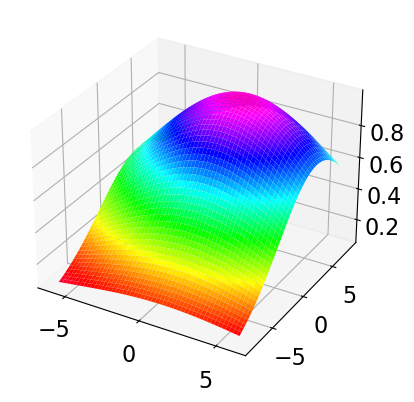
【例7.16】拟合曲面数据

利用模拟数据拟合曲面 z=e(x−μ1)2+(y−μ2)22δ2z = e \frac{(x-\mu_1)^2 + (y-\mu_2)^2}{2 \delta^2}，并画出拟合曲面的图形，要求分别使用函数 curve_fit, least_squares 和 leastsq 进行拟合，并做简单对比。

# Lec0319: 例7.16 拟合曲面数据
import numpy as np
from scipy.optimize import curve_fit, least_squares, leastsq
import pylab as plt

# 1. 数据预处理
np.random.seed(1)           # 为确保生成的伪随机序列相同，手动设置随机数种子
m, n = (200, 300)           # 定义插值分辨率
x = np.linspace(-6, 6, m)
y = np.linspace(-8, 8, n)
x2, y2 = np.meshgrid(x, y)
x3 = x2.flatten()
y3 = y2.flatten()
xy = np.vstack([x3, y3])

# 2. 拟合函数
zxy = lambda t, m1, m2, var: np.exp(-((t[0]-m1)**2+(t[1]-m2)**2)/(2*var**2))

z = zxy(xy, 1, 4, 6)                       # 无噪声函数值
zr = z+0.2*np.random.normal(size=z.shape)  # 噪声数据
coef = curve_fit(zxy, xy, zr)[0]           # 拟合参数
print("coef1:", coef)

zn=  zxy(xy, *p1)                          # 计算拟合函数的值
zn2 = np.reshape(zn, x2.shape)
ax = plt.axes(projection='3d')  #创建一个三维坐标轴对象
ax.plot_surface(x2, y2, zn2,cmap='gist_rainbow')

coef0 = np.random.randn(3)  #拟合参数的初值
fun = lambda t, x, y: np.exp(-((x-t[0])**2 +(y-t[1])**2)/(2*t[2]**2))
err = lambda t, x, y, z: fun(t,x,y)- z  #定义误差向量
coef2 = least_squares(err, coef0, args=(x3, y3, zr))
print('coef2:', coef2)
coef3 = leastsq(err, coef0, args=(x3,y3,zr))
print('coef3:', coef3)
plt.show()


coef1: [0.9962754  4.00604227 6.01024171]
coef2:      message: `ftol` termination condition is satisfied.
     success: True
      status: 2
         fun: [-3.243e-01  1.229e-01 ... -9.811e-03  1.269e-01]
           x: [ 9.963e-01  4.006e+00  6.010e+00]
        cost: 1203.3215859180655
         jac: [[-1.338e-02 -2.295e-02  6.143e-02]
               [-1.342e-02 -2.322e-02  6.187e-02]
               ...
               [ 7.824e-02  6.322e-02  1.064e-01]
               [ 7.854e-02  6.269e-02  1.071e-01]]
        grad: [-2.463e-07  5.357e-08 -9.862e-07]
  optimality: 9.862281413752783e-07
 active_mask: [ 0.000e+00  0.000e+00  0.000e+00]
        nfev: 8
        njev: 8
coef3: (array([0.9962754 , 4.00604227, 6.01024171]), 1)

【第03讲】插值和拟合 返回首页

【例7.1】待定系数法插值

【例7.2（续例7.1）】 用Lagrange插值再求例7.1的问题

【（续例7.1）】 用牛顿插值再求例7.1的问题

【例7.3】 龙格振荡

【例】 分段插值

几种插值算法的对比

【例7.4】 机床加工

【例7.5】三次样条插值

【例7.6】 欧洲地图的面积和周长

【例7.7】高线图和三维表面图

【例7.8】丘陵地带的高程测量

【例7.9】海域地形和等高线图

【例7.10】刀具磨损速度研究

【例7.11】求解行星运行轨道

【例7.12】约束线性最小二乘的拟合

【例7.13】单分子化学反应速度

【例7.14（续例7.13）】单分子化学反应速度（非线性拟合）

【例7.15】二维数据拟合

【例7.16】拟合曲面数据

≡