【案例01】黄河小浪底调水调沙问题 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Python3.11
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用，请勿用作商用。

最后更新：2024年3月2日

【知识点】

插值与拟合

【问题描述】

1. [习题2.9-P52] 求下列方程组的符号解和数值解：

2004年6月至7月黄河进行了第三次调水调沙试验，特别是首次由小浪底、三门峡和万家寨三大水库联合调度，采用接力式防洪预泄放水，形成人造洪峰进行调沙试验获得成功。整个试验期为20多天，小浪底从6月19日开始预泄放水，直到7月13日恢复正常供水结束。小浪底水利工程按设计拦沙量为75.5亿m3，在这之前，小浪底共积泥沙达14.15亿t。这次调水调沙试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪，在小浪底形成人造洪峰，冲刷小浪底库区沉积的泥沙，在小浪底水库开闸泄洪以后，从6月27日开始三门峡水库和万家寨水库陆续开闸放水，人造洪峰于29日先后到达小浪底，7月3日达到最大流量2700m3/s，使小浪底水库的排沙量也不断地增加。表1是由小浪底观测站从6月29日到7月10检测到的试验数据。

表1 观测数据（单位：水流量为m3/s，含沙量为kg/m3）
日期 6.29 - 6.30 - 7.1 - 7.2 - 7.3 - 7.4 -
时间 8:00 20:00 8:00 20:00 8:00 20:00 8:00 20:00 8:00 20:00 8:00 20:00
水流量 1800 1900 2100 2200 2300 2400 2500 2600 2650 2700 2720 2650
含沙量 32 60 75 85 90 98 100 102 108 112 115 116
日期 7.5 - 7.6 - 7.7 - 7.8 - 7.9 - 7.10 -
时间 8:00 20:00 8:00 20:00 8:00 20:00 8:00 20:00 8:00 20:00 8:00 20:00
水流量 2600 2500 2300 2200 2000 1850 1820 1800 1750 1500 1000 900
含沙量 118 120 118 105 80 60 50 30 26 20 8 5

要求根据实验数据建立数学模型研究下列问题：
1. 给出估计任意时刻的排沙量及总排沙量的方法；
2. 确定排沙量与水流量的关系。

【答案与解析】

1. 给出估计任意时刻的排沙量及总排沙量的方法

已知给定的观测时刻是等间距的，以6月29日零时刻开始计时，则各次观测时刻（离开始时刻6月29日零时刻的时间）分别为

ti=3600(12i−4),i=1,2,...,24t_i = 3600(12i - 4), i = 1, 2, ..., 24

其中计时单位为秒。第1次观测的时刻 tit_i = 28800，最后一次观测的时刻 t24=28800t_{24} = 28800。

记第 i 次观测时水流量为 viv_i，含沙量为 cic_i，则第 ii 次观测时的排沙量为 yi=civiy_i = c_i v_i。有关的数据如下：
节点 1 2 3 4 5 6 7 8
时刻 28800 72000 115200 158400 201600 244800 288000 331200
排沙量 57600 114000 157500 187000 207000 235200 250000 265200
节点 9 10 11 12 13 14 15 16
时刻 374400 417600 460800 504000 547200 590400 633600 676800
排沙量 286200 302400 312800 307400 306800 300000 271400 231000
节点 17 18 19 20 21 22 23 24
时刻 720000 763200 806400 849600 892800 936000 979200 1022400
排沙量 160000 111000 91000 54000 45500 30000 8000 4500

考虑到实际中的排沙量应该是时间的连续函数，为了提高模型的精度，采用三次样条函数进行插值。利用Python，可以通过numpy直接求出利用三次样条插值函数指定时刻的排沙量与时间的关系：y=y(t)y=y(t)，然后，再利用积分：

z=∫t1t24y(t)dtz = \int^{t_{24}}_{t_1} y(t) dt

即可得到总的排沙量等于 （1.844×108t）（1.844×10^8t）。

# ch0301-1
# 黄河小浪底调水调沙问题

import numpy as np
from scipy.interpolate import interp1d
import pylab as plt

# Q1：给出估计任意时刻的排沙量及总排沙量的方法  
a = np.loadtxt('../data/ch0301/ch0301.txt')
water = a[::2,:].flatten()   # 提出水流量并按照顺序变成行向量, ::2以偶数间隔取元素
sand = a[1::2,:].flatten()  # 提出含沙量并按照顺序变成行向量

y = sand * water   #计算排沙量
i = np.arange(1, 25) 
t = (12*i-4)*3600
t1 = t[0]
t2 = t[-1]
f = interp1d(t, y, 'cubic')      #进行三次样条插值
tt = np.linspace(t1, t2, 50000)  #取的插值节点
sandTotal = np.trapz(f(tt), tt)         #求总含沙量的数值积分
print('总含沙量为：', sandTotal)

总含沙量为： 184396665708.009

2. 确定排沙量与水流量的关系。

为了便于研究排沙量和水流量的关系，可以先对数据进行可视化处理，将排沙量与水流量的关系绘制成图。

# Project01-2
# 绘制出水流和排沙量的关系图
plt.rcParams['font.family'] = 'Microsoft YaHei'

plt.figure(figsize=(10, 3))  
plt.subplot(121); 
plt.plot(water[:11], y[:11], '*')
plt.title('Stage 1')
plt.xlabel('水流量$(m^3/s)$')
plt.ylabel('排沙量$(kg/m^3)$')
plt.subplots_adjust(wspace=0.3)
plt.subplot(122)
plt.plot(water[11:], y[11:], '*')
plt.gca().invert_xaxis()  
plt.title('Stage 2') 
plt.xlabel('水流量$(m^3/s)$')
plt.ylabel('排沙量$(kg/m^3)$')

Text(0.5, 0, 'Stage 2')

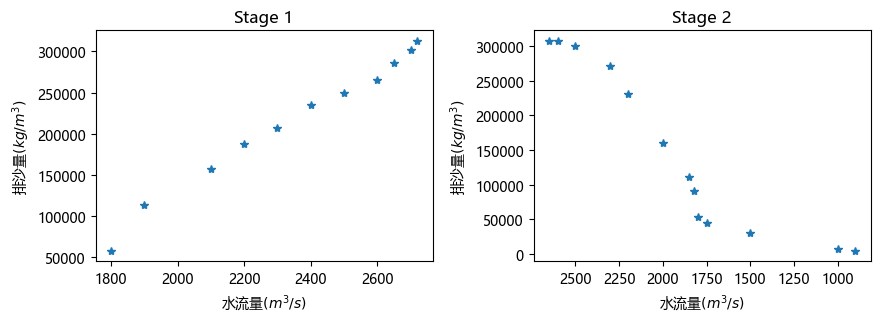
从试验数据可以看出，开始排沙量是随着水流量的增加而增长，而后是随着水流量的减少而减少。显然，变化规律并非是线性的关系，为此，把问题分为两部分分别研究水流量和排沙量的关系，从开始水流量增加到最大值 2720m3/s2720m^3/s 为第一阶段（即增长的过程），从水流量的最大值到结束为第二阶段。

两个阶段都接近线性，为了更准确，可以考虑同时使用一次和二次曲线来拟合，并用标准差来进行模型选择。
 最后，再根据标准差来进行模型选择。

# ch0301-3
rmse1 = np.zeros(2)  #第一阶段剩余标准差初始化
rmse2 = np.zeros(2)  #第二阶段剩余标准差初始化
print('第一阶段：')
for i in range(1,3):
    nh1 = np.polyfit(water[:11], y[:11], i)  #拟合多项式
    print('{} 次多项式系数:{}'.format(i, nh1))
    yh1 = np.polyval(nh1, water[:11])  #求预测值
    cha1 = sum((y[:11]-yh1)**2)  #求误差平方和
    rmse1[i-1] = np.sqrt(cha1/(10-i))
print('剩余标准差分别为：', rmse1)

print('第二阶段：')
for i in range(1,3):
    nh2 = np.polyfit(water[11:], y[11:], i)  #拟合多项式
    print('{} 次多项式系数:{}'.format(i, nh2))
    yh2 = np.polyval(nh2, water[11:])  #求预测值
    cha2 = sum((y[11:]-yh2)**2)  #求误差平方和
    rmse2[i-1] = np.sqrt(cha2/(12-i))
print('剩余标准差分别为：', rmse2)
plt.show()

第一阶段：
1 次多项式系数:[ 2.50565486e+02 -3.73384466e+05]
2 次多项式系数:[-5.82350463e-02  5.16415287e+02 -6.71064432e+05]
剩余标准差分别为： [10113.89642666  9284.01435752]
第二阶段：
1 次多项式系数:[ 2.02434781e+02 -2.39534846e+05]
2 次多项式系数:[ 1.06659104e-01 -1.80466799e+02  7.24210982e+04]
剩余标准差分别为： [45916.36419819 30962.39094986]

从结果来看，无论是第一阶段，还是第二阶段二次多项式的拟合效果都比一次多项式要好（标准差更小），因此，最终选择二次多项式来进行模型拟合。

y=−0.0582v2+516.4153v−671064.432y = -0.0582v^2+516.4153v - 671064.432

y=0.1067v2−180.4668v+72421.0982y = 0.1067v^2 - 180.4668v +72421.0982

PS：请大家自行尝试三阶、四阶以及更高阶的标准差，并判断哪种多项式最好。

【拓展练习】黄河水沙监测数据分析

（2023 年高教社杯全国大学生数学建模竞赛 E题）

黄河是中华民族的母亲河。研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变化和人民生活的影响，以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾等方面都具有重要的理论指导意义。

附件1 给出了位于小浪底水库下游黄河某水文站近 6 年的水位、水流量与含沙量的实际监测数据，附件2 给出了该水文站近 6 年黄河断面的测量数据，附件3 给出了该水文站部分监测点的相关数据。请建立数学模型研究以下问题：

问题1 研究该水文站黄河水的含沙量与时间、水位、水流量的关系，并估算近 6 年该水文站的年总水流量和年总排沙量。

问题2 分析近 6 年该水文站水沙通量的突变性、季节性和周期性等特性，研究水沙通量的变化规律。

问题3 根据该水文站水沙通量的变化规律，预测分析该水文站未来两年水沙通量的变化趋势，并为该水文站制订未来两年最优的采样监测方案（采样监测次数和具体时间等），使其
既能及时掌握水沙通量的动态变化情况，又能最大程度地减少监测成本资源。

问题4 根据该水文站的水沙通量和河底高程的变化情况，分析每年 6-7 月小浪底水库进
行“调水调沙”的实际效果。如果不进行“调水调沙”，10 年以后该水文站的河底高程会如何？

附件
附件1 2016-2021 年黄河水沙监测数据
附件2 黄河断面的测量数据
附件3 黄河部分监测点的监测数据

附录说明:
(1) “水位”和“河底高程”均以“1985 国家高程基准”（海拔 72.26 米）为基准面。
(2) 附件中的“起点距离”以河岸边某定点作为起点。

【案例01】黄河小浪底调水调沙问题 返回首页

【知识点】

【问题描述】

【答案与解析】

【拓展练习】黄河水沙监测数据分析

≡