【案例02】药物中毒急救 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Python3.11
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用，请勿用作商用。

最后更新：2024年3月10日

---

【知识点】

微分方程模型

一、问题描述

一天夜晚，你作为见习医生正在医院内科急诊室值班，两位家长带着一个孩子急匆匆进来，诉说两个小时前，孩子一口气误吞下了11片治疗哮喘病的、剂量为每片100mg的氨茶碱片，已经出现呕吐、头晕等不良症状。按照药瓶使用说明书，氨茶碱的每次用量成人是 $100 \sim 200mg$，儿童是 $3 \sim 5mg/kg$。如果服用过量，可使血药浓度（单位血液容积中的药量）过高，当血药浓度达到 $100 \mu g/ml$ 时，会出现严重中毒，达到 $200 \mu g/ml$ 则会致命。

作为一名医生，你清楚地知道，由于孩子服药是在两小时前，现在药物已经从胃进入肠道，无法再用刺激呕吐的办法排除。当前需要作出判断的是，孩子的血药浓度会不会达到 $100 \mu g/ml$，甚至是 $200 \mu g/ml$，如果会达到，则临床上应采取紧急方案来就救治孩子。

类似问题：

二、问题调查与分析

1. 人体血液的基本情况 人体服用一定药物后，血液浓度与人体的血液总量有关。一般来说，血液总量约位体重的 $7\% \sim 8\%$，即体重 $50 \sim 60kg$ 的成年人血液总量约为 4000mL。目测这个孩子的体重约为成年人的一半（提出假设或称量确定），可认为其血液总量约为 $2000mL$。由此，血液系统中的血药浓度与药量之间可以互相转换。

2. 药物转移的过程 药物口服后迅速进入胃肠道，再由胃肠道的外壁进入血液循环系统，被血液吸收。胃肠道中药物的转移率，即血液系统的吸收率，一般与胃肠道中的药量（设为 $x(t)$）成正比。药物在血液吸收的同时，又通过代谢作用由肾脏排出体外，排除率一般与血液中的药量（设为 $y(t)$）成正比。如果认为整个血液系统内药物的分布，即血药浓度是均匀的，可以将血液系统看作是一个房室，建立所谓的一室模型。基于以上思想，我们可以得到药物转移过程的示意图如下：

血液系统对药物的吸收率和排除率可以由半衰期确定，从药品的说明书可知，氨茶碱吸收的半衰期为 $5h$，排除的半衰期为 $6h$。（PS：半衰期是指某种物质衰变至原来数量的一半所需的时间。例如，在放射性衰变中，半衰期是指放射性物质衰变至原来数量的一半所需的时间；在医学领域，药物的半衰期指的是药物在血液中浓度降低一半所需的时间，或者药物自体内消除一半所需的时间。这个指标有助于医生确定药物的给药频率和剂量，以及计算多剂量给药中到达稳态浓度所需的时间。）

3. 施救方案 如果血液浓度达到危险水平，临床上施救的一种方法是采用口服活性炭来吸附药物，可使药物的排除率增加到原来（人体自身）的 $2$ 倍，另一种办法是进行体外血液透析，药物排除率可增加到原来的 $6$ 倍，但是安全性不能得到充分保证，建议尽量少用。

三、模型假设

为了判断孩子的血药浓度会不会达到危险水平，需要寻求胃肠道和血液系统中的药量随时间变化的规律。记胃肠道中的药量为 $x(t)$，血液系统中的药量为 $y(t)$，时间 $t$ 以孩子误服药的时刻为起点 $t = 0$。根据前面的调查与分析可作以下假设：

1. 胃肠道药中药物向血液系统输出的速率与胃肠道中的药量 $x(t)$ 成正比，比例系数记作 $\lambda(>0), t=0$ 时总剂量 1100mg 的药物在 $t=0$ 瞬间进入胃肠道（初态）。
2. 血液系统中的药物向体外输出的速率与血液系统中的药量 $y(t)$ 成正比，比例系数记作 $\mu(>0), t=0$ 时血液中无药物（初态）。
3. 氨茶碱被吸收的半衰期为 $5h$，排除的半衰期为 $6h$。
4. 孩子的血液总量为 $2000mL$。

四、建立模型

根据假设对胃肠道中药量 $x(t)$ 和血液系统中的药量 $y(t)$ 建立如下模型：

1. 由假设1可知，$x(0) = 11×100mg = 1100mg$，随着药物从胃肠道向血液系统的转移，因胃肠道中的药物逐渐减少，所以其转移量也逐渐减小。也就是说，$x(t)$ 下降的速度与 $x(t)$ 本身的大小成正比（比例系数为 $\lambda$），所以 $x(t)$ 满足微分方程：

$$\frac{dx}{dt} = - \lambda x, x(0) = 1100 \tag{1}$$

2. 由假设2可知，$y(0) = 0mg$，随着药物从血液系统向体外血液透析的转移，血液系统中的药物逐渐减少，也就相当于血液系统对药物的吸收，$y(t)$ 由于吸收作用而增长的速度就是 $\lambda x$，由于排除而减少的速度与 $y(t)$ 本身成正比（比例系数 $\mu > 0$），所以 $y(t)$ 满足微分方程：

$$\frac{dy}{dt} = \lambda x - \mu y, y(0) = 0 \tag{2}$$

方程（1）（2）中的参数 $\lambda, \mu$ 分别表示药物在胃肠道和血液系统中的转移速率，它们可以由假设3中药物的半衰期确定。

五、模型求解

5.1 药物吸收（胃肠道向血液系统转移）

微分方程（1）是可分离变量方程，通过求解可以得到：

$$x(t) = 1100 e^{-\lambda t} \tag{3}$$

其中胃肠道中的药量 $x(t)$ 随时间 $t$ 单调减少并趋于0。为了确定超参数 $\lambda$，我们可以利用药物吸收的半衰期为 5h，即 $x(5) = x(0)/2$，也即 $1100e^{-5 \lambda} = 1100/2$。由此可得 $\lambda = \ln(2)/5 = 0.1386 (1/h)$。此时，公式（3）可简化为：

$$x(t) = 1100 e^{-0.1386 t} \tag{4}$$

下面给出Python求解微分方程方程（1）得到解（3）的Python代码。此处，我们使用sympy符号计算方法进行化简，然后代入初值 $x(0) = 1100$，以获得公式（3）。

from sympy import symbols, Eq, dsolve, Function  

# 1. 定义变量  
t = symbols('t')
lamb = symbols('lambda')

# 2. 定义函数  
x = Function('x')(t)  

# 3. 建立微分方程
diff_eq = Eq(x.diff(t), -lamb*x)  # dx/dt = -lambda*x  

# 4. 使用dsolve解微分方程，并按照初始条件进行化简 
solution = dsolve(diff_eq, x)
solution_with_condition = dsolve(diff_eq, x, ics={x.subs(t, 0): 1100}) 

# 5. 输出求解结果打印解  
print('solution = ', solution)
print('solution_with_condition = ', solution_with_condition)

solution =  Eq(x(t), C1*exp(-lambda*t))
solution_with_condition =  Eq(x(t), 1100*exp(-lambda*t))

整理一下以上代码的输出，可得：当初值 $x(0) = 1100$ 时，解得公式（3）：

$$x(t) = 1100 e^{-\lambda t}$$

5.2 药物排除（血液系统向体外转移）

将（3）代入方程（2），可以得到描述药物在血液系统中的一阶线性微分方程：

$$\frac{dy}{dt} = -\mu y + 1100 \lambda e^{-\lambda t} \tag{5}$$

求解可得：

$$y(t) = \frac{1100 \lambda}{ \lambda - \mu } (e^{- \mu t} - e^{- \lambda t}) \tag{6}$$

类似的，使用sympy符号计算方法进行化简，然后代入初值 $y(0) = 0$，求解获得公式（5）。

from sympy import symbols, Eq, dsolve, simplify, Function
from sympy import exp

# 1. 定义变量  
t = symbols('t')
lamb = symbols('lambda')
mu = symbols('mu')

# 2. 定义函数  
y = Function('y')(t)  

# 3. 建立微分方程
diff_eq = Eq(y.diff(t), - mu*y + 1100 * lamb * exp(-lamb * t))  # dy/dt

# 4. 使用dsolve解微分方程，并按照初始条件进行化简 
solution = dsolve(diff_eq, y)
solution_with_condition = dsolve(diff_eq, y, ics={y.subs(t, 0): 0}) 
# solution_with_condition = simplify(solution_with_condition)

# 5. 输出求解结果打印解  
print('solution = ', solution)
print('solution_with_condition = ', solution_with_condition)

solution =  Eq(y(t), C1*exp(-mu*t) - 1100*lambda*exp(-lambda*t)/(lambda - mu))
solution_with_condition =  Eq(y(t), 1100*lambda*exp(-mu*t)/(lambda - mu) - 1100*lambda*exp(-lambda*t)/(lambda - mu))

为了根据药物排除的半衰期为 6h 来确定排除率比例系数 $\mu$，可以考虑血液系统只对药物进行排除的情况，这时 $y(t)$ 满足方程：

$$\frac{dy}{dt} = - \mu y \tag{7}$$

设在某时刻 $\tau$，有 $y(\tau) = a$，即此时血液中的药物含量为 $a$。则：

$$y(t) = a e^{-\mu(t-\tau)}, t \geq \tau \tag{8}$$

利用 $y(\tau + 6) = a/2$，可得 $\mu = (\ln 2)/6 = 0.1155(1/h)$。

求解方程（7）的Python代码如下所示:

from sympy import symbols, Eq, dsolve, simplify, Function
from sympy import exp
import numpy as np 

# 1. 定义变量  
t = symbols('t')
lamb = symbols('lambda')
mu = symbols('mu')
tau = symbols('tau')

# 2. 定义函数  
y = Function('y')(t)  

# 3. 建立微分方程
diff_eq = Eq(y.diff(t), - mu*y)  # dy/dt

# 4. 使用dsolve解微分方程，并按照初始条件进行化简 
solution = dsolve(diff_eq, y)
solution_with_condition = dsolve(diff_eq, y, ics={y.subs(t, 'tau'): 'a'}) 
solution_with_condition = simplify(solution_with_condition)

# 5. 输出求解结果打印解  
print('solution_with_condition = ', solution_with_condition)

solution_with_condition =  Eq(y(t), a*exp(mu*(-t + tau)))

以上根据以上方程可得简化后的血液药物浓度微分方程，适当简化后可得解（8）：

$$y(t) = a e^{\mu (-t + \tau)} = a e^{-\mu(t - \tau)}$$

5.3 结果汇总

将 $\lambda=0.1386$ 和 $\mu = 0.1155$ 代入方程（3），（6）中，可得：

$$x(t) = 1100 e^{-0.1386 t} \tag{9}$$
$$y(t) = 6600(e^{-0.1155t} - e^{-0.1386t}) \tag{10}$$

以上公式可以表明血液系统中的药量 $y(t)$ 随时间先增后减，并在 $t_i$ 小时达到最大值，然后逐渐减小。

六、结果分析

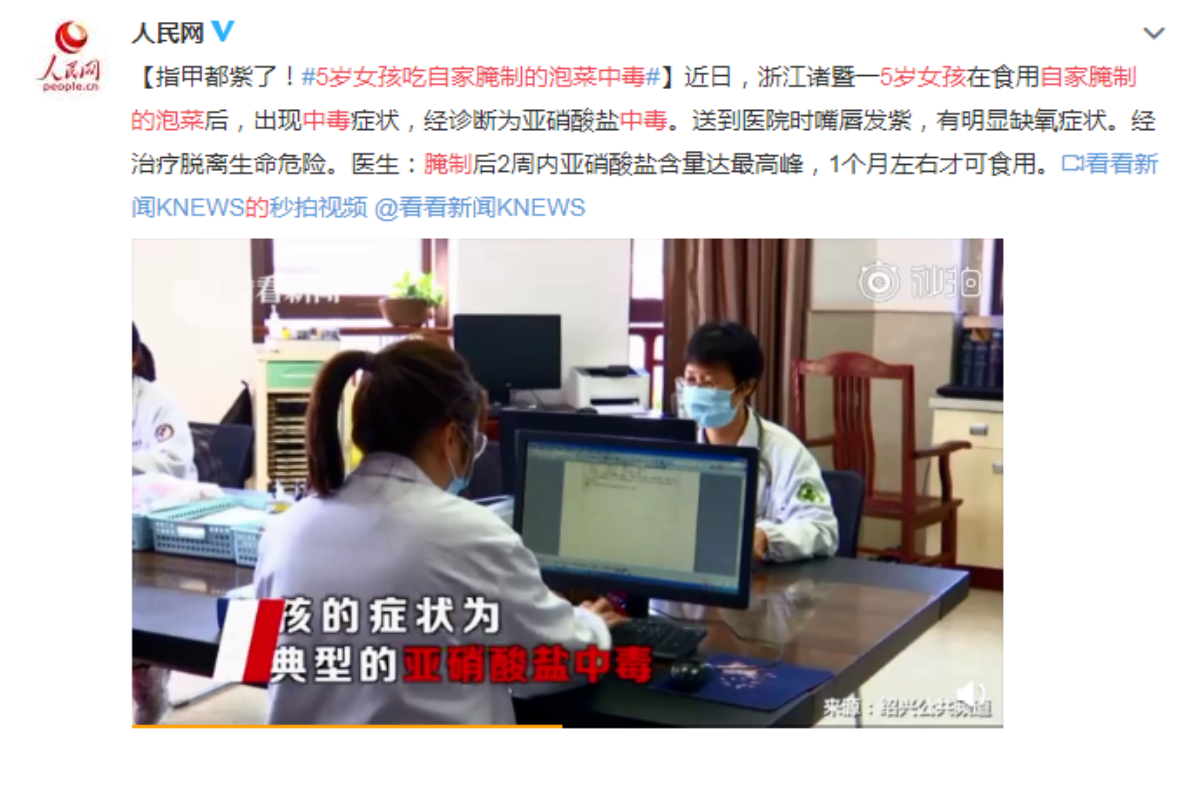
首先，我们使用Python根据公式（9）和（10）绘制出胃肠道中的药量 $x(t)$ 和血液系统中的药量 $y(t)$ 随时间的变化曲线，如 图1 所示。

import numpy as np
import matplotlib.pylab as plt

lamb = 0.1386
mu = 0.1155

xt = lambda t: 1100 * np.exp(-lamb * t)
yt = lambda t: 6600 * (np.exp(-mu * t) - np.exp(-lamb * t))
t0 = np.linspace(0, 20, 100)
plt.figure(figsize=(10,5))
plt.rc('font', size=16)
plt.plot(t0, xt(t0), '--', label='$x(t)$: Drag in the gut')
plt.plot(t0, yt(t0), label = '$y(t)$: Drug in the blood')
plt.legend()
plt.grid()
plt.xlabel('t/h')
plt.ylabel('x,y/mg')
plt.title('figure 1: No treatment')
plt.show()

根据假设4，孩子的血液总量为 2000mL，出现严重中毒的血液浓度 $100\mu g/ml$ 和致命的血液浓度 $200 \mu g/ml$ 分别相当于血液中药量 $y$ 达到 200mg 和 400mg。由 图1 看出，药量 y(t) 在约2h达到200mg，即孩子到达医院时已经出现严重中毒，如不及时施救，药量 y(t) 将在5小时（到达医院3h）达到致命剂量400mg，即孩子已经死亡。

由公式（10）容易精确地计算出孩子到达医院时血液系统中的药量 y(2) = 236.5mg，而计算药量达到400mg的时间（记作$t_1$），则需要解非线性方程 $y(t) = 6600(e^{-0.1155t} - e^{-0.1386t}) = 400$，用Python编程可得到 $t_1 = 4.87h$。

由 图1 还可以看出，血液中药量 $y(t)$ 达到最大值的时间约在 $t=8h$，即到达医院后6h，其精确值可也由方程（10）计算获得，记作 $t_2$：

$$t_2 = \frac{\ln(1+\lambda/6\mu)}{\lambda - \mu} = 7.89h$$

此时，$y(t_2) = 442.1mg$

from scipy.optimize import fsolve, fmin

y2 = yt(2)
print('2h时血液中的药量：', y2)
eq = lambda t: yt(t) - 400
t1 = fsolve(eq, 2)
print('药量在 {}h 时达到400mg。'.format(t1))
ytm = lambda t: -yt(t)     # 定义yt的相反数匿名函数
t2 = fmin(ytm, 2)
print('{} h 时达到最大药量 {}。'.format(t2, yt(t2)))

2h时血液中的药量： 236.52132678290988
药量在 [4.86585945]h 时达到400mg。
Optimization terminated successfully.
         Current function value: -442.065329
         Iterations: 21
         Function evaluations: 42
[7.89267578] h 时达到最大药量 [442.06532921]。

利用这个模型，还可以确定对于孩子及成人服用氨茶碱能引起严重中毒和致命的最小剂量问题（拓展练习）。

七、施救方案

根据上述分析，我们得出结论，若不即使施救，孩子会有生命危险。根据调查，如采用口服活性炭来吸附药物的办法进行施救，药物的排除率可增加到 $\mu$ 的2倍，即 $0.1155 × 2 = 0.231$；而采用体外血液透析的方法，药物排除率可增加到 $\mu = 0.1155×6 = 0.693$，血液中药量下降得更快。虽然血液透析能够更快排除药物，但该方法存在一定的危险性，而口服活性炭则相对简单且安全。在临床中究竟采取哪种方法进行救治需要我们给出响应的数据分析后，征求病人和家属的意见后再确定。

下面，我们给出使用口服活性炭进行施救的方案分析。

7.1 使用口服活性炭进行施救

设孩子到达医院时（t=2）就立即开始施救。前面已经算出 $y(2) = 236.5$，由（2）（3）可得到新模型：

$$\begin{cases} \frac{dz}{dt} & = \lambda x - \mu z, t \geq 2, \\ x & = 1100 e^{-\lambda t}, \\ z(2) & = 236.5 \end{cases} \tag{11}$$

其中，$z(t)$ 表示采用口服活性炭后，血液中的药量。不难发现，该模型依然是一个一阶线性微分方程，只不过初始时刻 $t=2$时，当 $\lambda = 0.1386$，而 $\mu = 0.2310$ 时，该方程（11）的解为：

$$z(t) = \frac{1100 \lambda}{\mu - \lambda} e^{-\lambda t} + c_2 e^{-\mu t} \tag{12}$$

利用初值 $z(2)=236.5$，可以得到解的简化表达式：

$$z(t) = 1650 e^{-0.1386t} - 1609.5 e^{-0.2310t}, t \geq 2 \tag{13}$$

t = symbols('t')
lamb = 0.1386
mu2 = 0.2310

z = Function('z')(t)

diff_eq2 = Eq(z.diff(t), -mu2*z + 1100 * lamb * exp(-lamb * t))   #dz/dt
solution2 = dsolve(diff_eq2, z)
solution2_with_condition = dsolve(diff_eq2, z, ics={z.subs(t, 2): 236.5})

# 5. 输出求解结果打印解  
print('solution = ', solution2)
print('solution_with_condition = ', solution2_with_condition)

solution =  Eq(z(t), C1*exp(-0.231*t) + 1650.0*exp(-0.1386*t))
solution_with_condition =  Eq(z(t), -1609.52988961616*exp(-0.231*t) + 1650.0*exp(-0.1386*t))

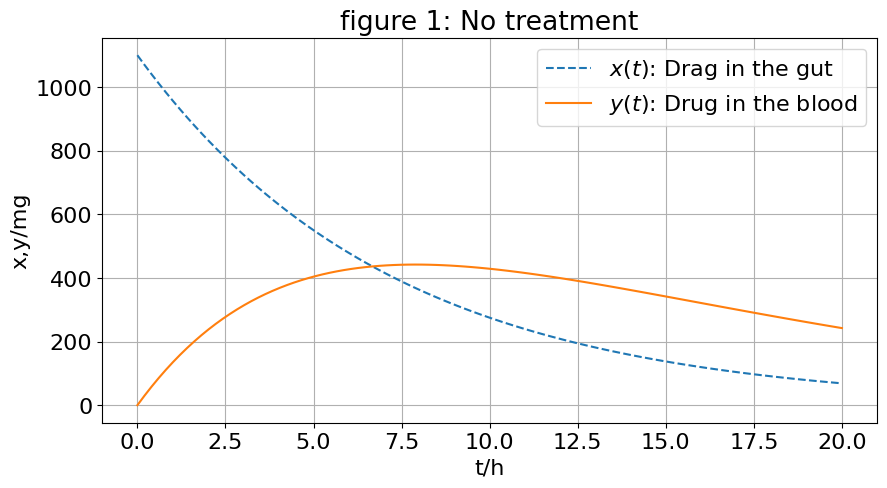
使用Python对公式（13）作图得 图2。

zt = lambda t: -1609.5 * np.exp(-0.231 * t) + 1650 * np.exp(-0.1386 * t)

t2 = np.linspace(2, 20, 100)
plt.figure(figsize=(10,5))
plt.rc('font', size=16)
plt.plot(t0, xt(t0), '--', label='$x(t)$: Drag in the gut')
plt.plot(t2, zt(t2), label = '$z(t)$: Drug in the blood')
plt.legend()
plt.grid()
plt.xlabel('t/h')
plt.ylabel('x, z/mg')
plt.title('figure 2: Activated carborn')
plt.show()

由图2可以看出，施救后血液中药量 $z(t)$ 达到最大值的时间约在 $t=5h$，即到达医院施救后3h，其精确值可由公式（8）计算获得，记作 $t_3$。$t_3 = 5.26h$，且 $z(t_3) = 318.4mg$，远低于 $y(t)$ 的最大值和致命水平。

图2还表明，虽然采用了口服活性炭吸附药物的办法进行施救，但血液中药量 $z(t)$ 仍有一段时间在上升，说明用这种方法药物的排除率增加还不够大。不妨计算一下，如果要使 $z(t)$ 在施救后 ($t \geq 2$) 立即下降，排除率 $\mu$ 至少应该多大。

z(t) 在 $t=2$ 取得最大值，相当于 $t=2$ 时，公式（7）满足：

$$\frac{dz}{dt} |_{t=2} = (\lambda x - \mu z)|_{t=2} = 0 \tag{9}$$

由（5）算出 $x(2) = 833.7$，再利用前面已有的 $z(2) = 236.5$ 和 $\lambda = 0.1386$，立即得到 $\mu = 0.4885$，约原来（人体自身 $\mu=0.1155$）的 $4.2$ 倍。此时，如果采用血液透析法，由于它可使排除率增加到6倍，它确实可以有效抑制药物中毒。但在临床中，血液透析的安全性依然是需要考虑的重要因素之一。

from scipy.optimize import fsolve, fmin

ztm = lambda t: -zt(t)     # 定义yt的相反数匿名函数
t3 = fmin(ztm, 2)
print('{} h 时达到最大药量 {} mg。'.format(np.round(t3[0], 4), np.round(zt(t3)[0], 4)))

x2 = xt(2)
mu3 = x2*lamb/y2
n = mu3/mu
print('药量不增加时，排除率达到 mu = {:.4f} 时，才能快速排除危险，\n 此时排除率为人体自身排除率的 {:.4f} 倍。'.format(mu3, mu3/mu))

Optimization terminated successfully.
         Current function value: -318.390614
         Iterations: 19
         Function evaluations: 38
5.2595 h 时达到最大药量 318.3906 mg。
药量不增加时，排除率达到 mu = 0.4885 时，才能快速排除危险，
 此时排除率为人体自身排除率的 4.2298 倍。

7.2 使用血液化疗进行施救

...请读者自行补充完成

【拓展练习】 安全服用药物的最小剂量问题

1. 利用药物中毒施救模型确定对于孩子（血液总量2000mL）及成人（血液总量为4000mL）服用氨茶碱能引起严重中毒和致命的最小剂量。
2. 如果采用的是体外血液透析的办法，求解药物中毒施救模型的血液中药量的变化规律并作图。