【案例03】传染病模型和SARS的传播 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Python3.11
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用，请勿用作商用。

最后更新：2024年4月7日

---

【知识点】

微分方程、差分方程

本教案将用数学建模的方法来研究如下问题：

1. 建立传染病的数学模型描述传染病的传播过程
2. 分析感染人数的变化规律，预测传染病高峰的到来
3. 探索控制、根除、预防传染病传播蔓延的手段

流行病学中的一大类模型，称为“舱室”模型，它是将人群分成若干个“舱室”，各个舱室之间会有转移率（变化率），用数学模型语言来描述整个系统，就得到一个微分方程组，但往往是没有解析解的，这就需要利用 Python 进行数值求解。

一、问题提出

2002年冬到2003年春，一种名为SARS（severe acute respiratory syndrome, 严重急性呼吸道综合症，民间俗称非典）的传染病肆虐全球。SARS首发于中国广东，迅速扩散到东南亚乃至30多个国家和地区，包括医务人员在内的多名患者死亡，引起社会恐慌、媒体关注以及各国政府和联合国、世界卫生组织的高度重视、积极应对，直至最终疫情的蔓延。突如其来的SARS及其迅猛的传播和严重的后果，成为21世纪的第一大社会热点事件。

SARS被控制住不久，2003年的全国大学生数学建模竞赛就以“SARS传播”命名当年的A题和C题，题目中要求“建立你们自己的模型；特别要说明怎样才真正预测以及能为预防和控制提供可靠、足够的信息的模型，这样做的困难是哪里？对于卫生部门所采取的措施做出评论，如：提前或延后5天采取严格隔离措施，对疫情传播所造成的影响做出估计。”题目还给出了北京市从2003年4月20日至6月23日逐日的疫情数据供参考（表1 是部分数据）。

表1 北京市的疫情数据 数据文件：Project03_SARS的传播。

日期	已确诊病例累计	现有疑似病例	死亡累计	治愈出院累计
4月20日	339	402	18	33
4月21日	482	610	25	43
4月22日	588	666	28	46
$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$
6月22日	2521	2	191	2257
6月23日	2521	2	191	2277

本教案先介绍数学、医学领域中基本的传染病模型，然后结合赛题，介绍几个描述、分析SARS传播过程的模型及求解结果。这些模型对于COVID-19新冠肺炎的传播与预测也同样适用。

二、传染病模型

虽然不同类型的传染病传播过程在医学上有其各自的特点，但是依然可以从数学建模的角度，按照一般的传播机理建立以下几种基本模型。

2.0 总体假设

先引入一些符号表示各“舱室”，对于简单的舱室模型，有这四类人群就足够了，为了进一步扩展模型也可以推广到更多的人群划分。

• S (Susceptible)易感者：指缺乏免疫能力健康人，与感染者接触后容易受到感染。
• E (Exposed)暴露者：指接触过感染者但暂无传染性的人，可用于存在潜伏期的传染病。
• I (Infectious)感染者：指有传染性的病人，可以传播给 S，将其变为 E 或 I。
• R (Recovered)治愈者：指治愈后或注射疫苗后具有免疫力的人，如终身免疫传染病，则不会再变为 S、E 或 I，如果免疫期有限，就可以重新变为 S 类，进而可被感染。

下面再给出一些常用的超参数假设：

• 时间 $t$：一般考虑离散时间，以天为最小时间单位。t 时刻各类人群占总人口的 比例 分别记为 $S(t), E(t), I(t), R(t)$；各类人数所占初始比率为 $S(0), E(0), I(0), R(0)$，分别简记为 $S_0, E_0, I_0, R_0$。
• 接触数 $\lambda$：每个感染者每天有效接触的易感者的平均人数。
• 发病率 $\delta$：每天感染成为感染者的暴露者占暴露者总数的比例。
• 治愈率 $\mu$：每天被治愈的感染者人数占感染者总数的比例。
• 平均传染期 $1/\mu$：从感染到治愈的平均天数。
• 传染期接触数 $\sigma=\lambda/\mu$：每个感染者在整个传染期内，有效接触的易感者人数。

其他总体假设：

1. 易感者与感染者发生有效接触即变为暴露者，暴露者经过平均潜伏期后成为感染者，感染者可被治愈成为治愈者，治愈者终身免疫不再成为易感者；
2. 总人口为 N，不考虑人口的出生与死亡，迁入与迁出，假设短期内总人口不变，对于长期传染病，也可以考虑总人口可变，即总人口按人口模型变化，比如 Logistic 模型。

2.1 指数传播模型

2.1.1 基本假设

（1）研究区域是一个封闭区域，在一个时期内人口总量 $N$ 相对稳定，不考虑人口的迁入与迁出，也不考虑人口的出生与死亡。
（2）$t$ 时刻染病人数 $N(t)$ 是随时间连续变化的、可微的函数。
（3）每个病人在单位时间内的有效接触（足以使人致病）或传染的人数为 $\lambda$（$\lambda > 0$ 为常数）。

2.1.2 模型建立与求解

记 $N(t)$ 为 $t$ 时刻染病人数，则 $t + \Delta t$ 时刻的染病人数为 $N(t + \Delta)$。从 $t \rightarrow t + \Delta t$ 时间内，净增加的染病人数为 $N(t + \Delta) - N(t)$，根据假设（3），有：

$$N(t + \Delta) - N(t) = \lambda N(t) \Delta t \tag{1}$$

若记 $t=0$ 时刻，染病人数为 $N_0$，则由假设（2），在上式两端同时除以 $\Delta t$，并令 $\Delta t \rightarrow 0$，得染病人数的微分方程预测模型：

$$\begin{cases} \frac{dN(t)}{dt} = \lambda N(t), t>0 \\ N(0) = N_0 \end{cases} \tag{2}$$

利用分离变量法，可以得到该模型的解析解：

$$N(t) = N_0 e^{\lambda t} \tag{3}$$

下面，我们分别给出数学解析中的 分离变量法 和 Python求解法：

• 数学解析法

考虑给定的微分方程：$\frac{dN(t)}{dt} = \lambda N(t), \quad t > 0$

以及初始条件：$N(0) = N_0$

首先将微分方程改写为：

$$\frac{1}{N(t)} \frac{dN(t)}{dt} = \lambda$$

接下来，对两边同时积分：

$$\int \frac{1}{N(t)} \frac{dN(t)}{dt} \, dt = \int \lambda \, dt$$

由于左边是对$\frac{1}{N(t)}$关于$N(t)$的导数进行积分，我们得到：

$$\ln |N(t)| = \lambda t + C$$

其中$C$是积分常数。

由于$N(t)$代表数量，它应该是非负的，因此我们可以去掉绝对值符号：

$$\ln N(t) = \lambda t + C$$

接下来，我们使用初始条件来求解积分常数 $C$。将 $t = 0$ 和 $N(0) = N_0$ 代入上式，我们得到：

$$\ln N_0 = \lambda \cdot 0 + C$$

从而解得：

$$C = \ln N_0$$

将$C$的值代回原方程，我们得到：

$$\ln N(t) = \lambda t + \ln N_0$$

利用对数的性质，我们可以将上式改写为：

$$\ln N(t) - \ln N_0 = \lambda t$$

$$\ln \left( \frac{N(t)}{N_0} \right) = \lambda t$$

最后，通过取指数，我们得到：

$$\frac{N(t)}{N_0} = e^{\lambda t}$$

从而解得：

$$N(t) = N_0 e^{\lambda t}$$

• Python求解法

from sympy import symbols, Eq, Function, dsolve, exp  

# 1. 定义变量和函数  
t, lambda_value, N0 = symbols('t lambda N0')  
N = Function('N')(t)  

# 2. 建立微分方程  
equation = Eq(N.diff(t), lambda_value * N)  

# 3. 使用dsolve求解特解，直接代入初始条件 N(0) = N0  
ics = {N.subs(t, 0): N0}          # 定义初始条件
particular_solution = dsolve(equation, N, ics=ics)  

# 4. 输出微分方程的特解  
particular_solution

$N(t) = N_0 e^{\lambda t}$

2.1.3 结果分析与评价

模型结果显示传染病的传播是按指数函数增加的。一般而已，在传染病发病初期，对传染源和传播路径未知，以及没有任何预防控制措施的情况下，这一结果是正确的。此外，我们注意到，当 $t \rightarrow \infty$ 时，$N(t) \rightarrow \infty$，这显然不符合实际情况。事实上，在封闭系统的假设下，区域内人群总量是有限的。预测结果出现明显失误。为了与实际情况吻合，有必要在原有基础上修改模型假设，以进一步完成模型。

2.2 SI模型

考虑总人口由感染者I（infective）和易感染者S（susceptible）两类人群构成，分别简称患者和健康人。在传染病模型中取两个词的英文字头称为SI模型。设所考察地区的总人数（N）不变，时刻 $t$ （单位：天）健康人和患者在总人数中的比例分别记作 $s(t)$ 和 $i(t)$，显然有 $s(t) + i(t) = 1$。

SI 模型最简单，适合不会反复发作的传染病。

2.2.1 基本假设

（1）假设1：在传播期内，所考察地区的人口总数 N 保持不变，即不考虑生死，也不考虑迁移。
该模型通常不适合长期传染病。
（2）假设2：人群分为感染者I（infective）和易感染者S（susceptible）两类，即患者和健康人。
（3）假设3：设 $t$ 时刻两类人群在总人口中所占的比例分别为 $s(t)$ 和 $i(t)$，则 $s(t) + i(t) = 1$。
（4）假设4：假设每个患者每天“有效接触”的易感者人数是常数 $\lambda$，称接触率，且当健康人被有效接触后立即倍感染者为患者，$\lambda$ 也称感染率，它反映了本地区的卫生防疫水平。
（5）假设5：假设人口总数足够大，只考虑传播过程中的平均效应，即函数 S(t) 和 I(t) 可以视为连续且可微的。

2.2.2 模型的建立

SI模型 的人群转移规律可以表示为下图：

根据以上假设，每个患者每天有效接触的健康人数是 $\lambda s(t)$，全部患者 $N·i(t)$ 每天有效接触的健康人数是 $N·i(t)·\lambda s(t)$，这些易感染的健康人立即被感染成患者，于是在 $t \rightarrow \Delta t$ 时间内，新增加的感染者人数为：

$$N(i(t+\Delta t) - i(t)) = N·i(t)·\lambda·s(t)·\Delta t \tag{4}$$

令 $\Delta t \rightarrow 0$，同时两边同时除以 $\Delta t$，得到满足微分方程的感染者比例 $i(t)$：

$$N · \frac{di(t)}{dt} = N·\lambda s(t) i(t) \tag{5}$$

进一步简化，约去 $N$，可得：

$$\frac{di(t)}{dt} = \lambda s(t) i(t) \tag{6}$$

由假设（3）可知，$s(t)=1-i(t)$，代入上式，得：

$$\frac{di(t)}{dt} = \lambda i(t)(1-i(t))\tag{7}$$

假设起始时刻 $t=0$，感染者占总人口的比例为 $i(0)=i_0$，于是 SI模型 可描述为：

$$\begin{cases} \frac{di(t)}{dt} = \lambda i(t)(1-i(t)), t>0 \\ i(0) = i_0 \end{cases} \tag{8}$$

2.2.3 模型求解

使用分离变量法或者Python符号法可以求解以上 SI模型 的微分方程。

from sympy import symbols, Eq, Function, dsolve, diff

# 1. 定义变量和函数  
i, lambda_value, i0, t = symbols('i lambda i0 t')  
I = Function('i')(t)  

# 2. 建立微分方程  
equation = Eq(diff(I, t), lambda_value * I * (1 - I))

# 3. 使用dsolve求解特解，直接代入初始条件 N(0) = N0  
ics = {I.subs(t, 0): i0}          # 定义初始条件
solution = dsolve(equation, I, ics=ics)  

# 4. 输出微分方程的特解
solution

$i(t) = \frac{1}{1+\frac{(1-i_0)e^{-\lambda t}}{i_0}}$

根据习惯，我们可以对以上结果进行进一步化简，得

$$i(t) = \frac{1}{1+(\frac{1}{i_0} - 1)e^{-\lambda t}} \tag{8}$$

2.2.4 结果分析与评价

在数学中，微分方程（8）是典型的 logistic 模型；在医学上，$\frac{di(t)}{dt} \sim t$ 为传染病曲线，它表示传染病人的增加率与时间的关系；感染人数和时间的关系则可以用 $i(t) \sim t$ 分布进行表示，不难看出它是一个 $S$ 形的Logistic增长曲线。在下面的Python代码中，我们分别设置两个超参数：$\lambda = 0.1$，$i_0 = 0.01$，代入模型（8），并进行求解来表示这两个曲线。

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
from scipy.interpolate import interp1d

# 1. 数据载入
lambda_value = 0.01               # 设置每个感染者每天感染人数，也即感染率
i0_value = 0.1                    # 设置初始感染者比例
t = np.linspace(0, 1000, 1000)    # 定义时间点数组

# 2. 模型定义
def func(I, t, lambda_):
    return lambda_ * I * (1 - I)

# 3. 拟合符号解及求解数值解
# 使用odeint求解微分方程
y0 = i0_value
solution_SI = odeint(func, y0, t, args=(lambda_value,))
# 计算 dI/dt
dI_dt_solution_SI = np.gradient(solution_SI[: ,0], t)
# 创建一个插值函数来平滑dI/dt的值
dIdt_SI = interp1d(t, dI_dt_solution_SI, kind='cubic')
max_dI_dt_SI = np.max(dI_dt_solution_SI)
max_t_SI = t[np.where(dI_dt_solution_SI == max_dI_dt_SI)]

# 绘制感染率曲线和感染速度曲线
plt.figure(figsize=(10, 4))
plt.subplot(1,2,1)
plt.plot(t, solution_SI)
plt.axhline(y=1.0, color='r', linestyle='--')   # 绘制一条参考线，表示全部人口均被感染
plt.xlabel('time $(t)$')
plt.ylabel('$i(t)$')
plt.title('Infectious disease curve')
plt.subplot(1,2,2)
plt.plot(t, dI_dt_solution_SI)
plt.plot(max_t_SI, max_dI_dt_SI, 'ob')
plt.text(max_t_SI+40, max_dI_dt_SI, '[' + str(np.round(max_t_SI[0], 2)) + ', ' + str(np.round(max_dI_dt_SI, 4)) + ']')
plt.axvline(x=max_t_SI, color='r', linestyle='--')
plt.xlabel('time $(t)$')
plt.ylabel('Dervative $di(t)/dt$')
plt.title('Infectious disease rate curve')
plt.subplots_adjust(wspace=0.3)
plt.show()

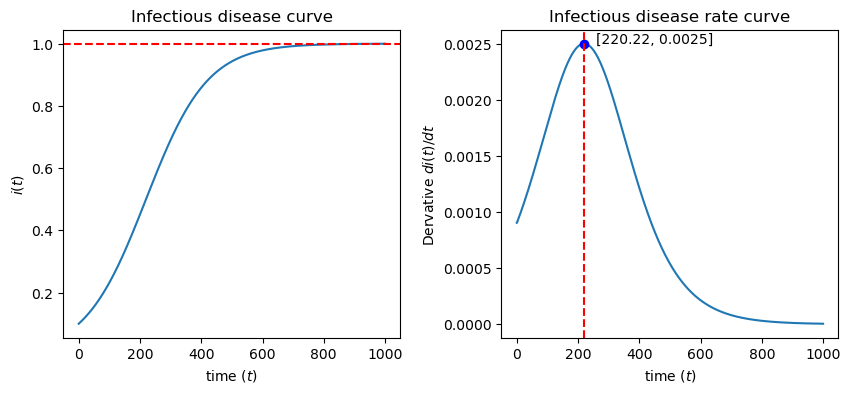
注意在上面的代码中，由于我们约去了总人数N，因此设置每天感染人数$\lambda$的时候，实际上是以 单位1作为参考值，也即此处的 $\lambda$ 也是一个感染率比例值。

从左边的感染者比例曲线可以看出，感染人数 $i(t)$ 从 $t=0$ 时的 $i_0=0$ 迅速上升，通过曲线的拐点后上升变缓，当 $t \rightarrow \infty$ 时 $i(t) \rightarrow 1$，即所有健康人终将被感染成患者。该模型的缺陷是显而易见的，因为它并不符合实际情况。究其原因，是SI模型只考虑了感染者和易感染着这两种人群的情况，健康人可以被感染，而没有考虑到感染者可以被治愈的情况。

从右边的感染速度曲线，我们可以发现感染的速度是随着时间 $t$ 的推移先增加后减少的，这是比较符合实际情况。当 $t=t_{max}$ 时，疫情最为猛烈，感染者的增长速度也是最快的。显然$t_{max}$ 与 $\lambda$ 成反比。根据微分方程（8），很容易得出结论，当 $i(t)=0.5$ 时，增长速率 $\frac{di(t)}{dt}$ 达到最大值，将该设定代入公式（9），可以得到传染病高峰时刻为：

$$t_{max} = \frac{\ln (1/I_0 - 1)}{\lambda} \tag{10}$$

由于 $\lambda$ 表示的是疾病的传染率，它反映了当地的医疗卫生水平，$\lambda$ 越小，医疗卫生水平越高，传染的高峰时刻来临的也就越晚。所以改善保健设施，提高医疗卫生水平，降低 $\lambda$ 值就可以推迟传染高潮的到来。

以上分析结论，读者可以通过调节超参数 $\lambda, i_0$ 来进行验证。

在下面的模型中，我们将增加关于患者被治愈的情况。

2.3 SIS模型

2.3.1 基本假设

有些传染病如伤风、痢疾等，虽然可以治愈，但治愈后基本没有免疫力，于是患者治愈后又变成易感染的健康人。由此将这个模型称为SIS模型。

SIS模型 只需要在 SI模型 的假设基础上增加一个假设条件即可.

假设6：患者每天被治愈的人数比例是常数 $\mu$，称治愈率。
假设7：病人被治愈后成为仍可被感染的健康人。

2.3.2 模型的建立

SIS模型 的人群转移规律可以表示为下图：

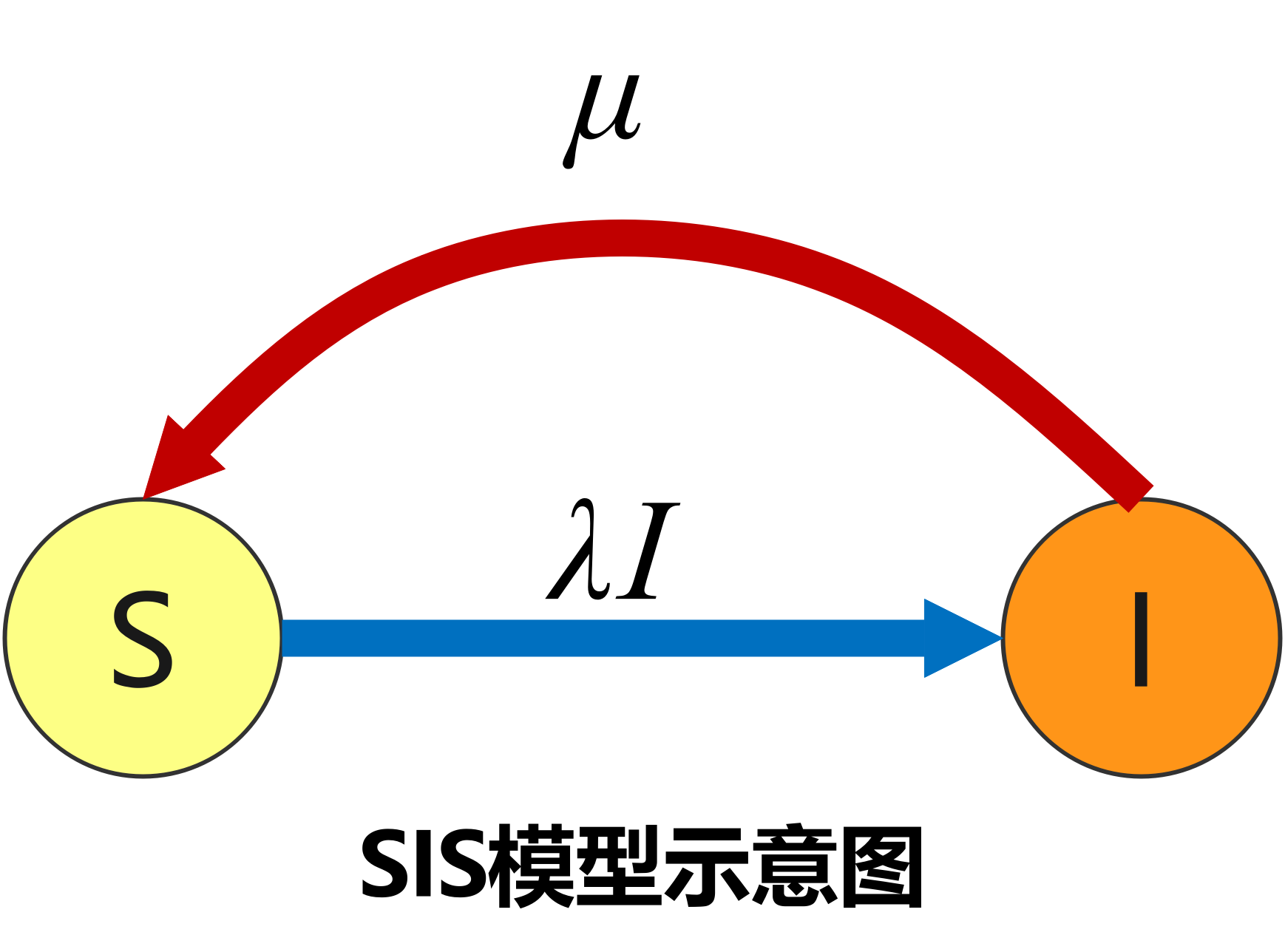
根据 假设6，每天新增的感染者人数 $N \lambda s(t) i(t)$，应该减去每天被治愈的感染者人数 $N i(t) \mu$，同时除以 $N$ 后可得：

容易知道，增加了这个假设后，方程（5）的右端应该减去每天被治愈的患者数 $N_{\mu i}$，于是有（同样约去方程两端的N）

$$\frac{di(t)}{dt} = \lambda s (t)i(t) - \mu i(t) \tag{11}$$

于是我们可以得到修正后的 SIS模型：

$$\begin{cases} \frac{di(t)}{dt} = \lambda i(t)(1-i(t)) - \mu i(t), t>0 \\ i(0) = i_0 \end{cases} \tag{12}$$

若令：

$$\sigma = \lambda / \mu \tag{13}$$

同时将 $s(t) = 1-i(t)$ 和 $\mu = \lambda / \sigma$ 代入（12）式，可得 SIS模型 的另一种形式：

$$\begin{cases} \frac{di(t)}{dt} = \lambda i(t)((1-\frac{1}{\sigma}) - i(t)), t>0 \\ i(0) = i_0 \end{cases} \tag{14}$$

检查公式（13）可知，因为 $\mu$ 是治愈率，因此 $1/\mu$ 可以视为平均传染期（即感染者被治愈所需的平均时间），而 $\lambda$ 是感染率，所以 $\sigma$ 可以用来表示整个感染期内每感染者有效接触而感染的平均（健康）人数，即 传染期的接触数，或 感染数。

2.3.3 模型求解

公式（14）给出的微分方程可以使用分离变量法进行求解，但由于计算较复杂，我们使用以下Python来求解方程的解析解。此处令 $k = 1- \frac{1}{\sigma}$。

from sympy import symbols, Eq, Function, dsolve, diff, simplify, expand

# 1. 定义变量和函数  
i, lambda_value, k, i0, t = symbols('i lambda k i0 t')  
I = Function('i')(t)  

# 2. 建立微分方程  
equation = Eq(diff(I, t), lambda_value * I * (k - I))

# 3. 使用dsolve求解特解，直接代入初始条件 i(0) = i0  
ics = {I.subs(t, 0): i0}          # 定义初始条件
solution = dsolve(equation, I, ics=ics)  

# 4. 输出微分方程的特解
simplify(solution)

$i(t) = \frac{i_0 k e^{k \lambda t}}{i_0 e^{k \lambda t} - i_0 + k}$

在以上的代码中，如果我们假设治愈率等于感染率，即 $\lambda=\mu$，此时相当于感染者的增长只和感染率相关。（注意此时的感染率 $\lambda$ 是经过治愈率修正后的感染率，并不是初始的 $\lambda_0$）。下面给出 $\lambda=\mu$，也即 $\sigma=1$时的方程求解过程。

from sympy import symbols, Eq, Function, dsolve, diff, simplify, expand

# 1. 定义变量和函数  
i, lambda_value, i0, t = symbols('i lambda i0 t')  
I = Function('i')(t)  

# 2. 建立微分方程  
equation = Eq(diff(I, t), lambda_value * I * ( - I))

# 3. 使用dsolve求解特解，直接代入初始条件 i(0) = i0  
ics = {I.subs(t, 0): i0}          # 定义初始条件
solution = dsolve(equation, I, ics=ics)  

# 4. 输出微分方程的特解
simplify(solution)

$i(t) = \frac{i_0}{i_0 \lambda t + 1}$

由上面两段代码，我们可以得到微分方程(14)的解析解：

$$\begin{cases} i(t) = \frac{i_0 k e^{k \lambda t}}{i_0 e^{k \lambda t} - i_0 + k} &, \lambda \neq \mu \\\\ i(t) = \frac{i_0}{i_0 \lambda t + 1} &, \lambda = \mu \end{cases} \tag{15}$$

将（15）整理一下，并将 $k = 1- \frac{1}{\sigma}$ 代入后，可以得到SIS模型的解析解：

$$\begin{cases} i(t) = (1 - \frac{1}{\sigma} + (\frac{1}{i_0} - \frac{1}{1-\frac{1}{\sigma}}) e^{- \lambda (1-\frac{1}{\sigma} t)^{-1}} &, \lambda \neq \mu \\\\ i(t) = (\lambda t + \frac{1}{I_0})^{-1} &, \lambda = \mu \end{cases} \tag{16}$$

2.3.4 结果分析与评价

上面得到的解析解，为我们展示了感染者 $i(t)$ 与初始感染人数 $i_0$, 每个感染者有效接触人数 $\lambda$ 以及治愈率 $\sigma$ 之间的关系。从直观上很容易理解，感染者 $i(t)$ 与感染者在感染期内所接触的人数 $\sigma = \lambda / \mu$ 有直接的关系。若每个感染者在生病期间因有效接触而感染的人数大于1，那么患者比例自然会增加，反之，患者比例会减少。所以，如果我们能在第一时间发现一个人被感染了，并且将其隔离，那么总感染人数必然持续减少，直至 $i(t)=0$。

下面，我们我们对这个 直观感觉 进行定量和可视化分析，我们分别做如下集中定义：
1). 模型1 传染病发生的初期，感染者较少，感染率较低，治愈率也较低。设 $i_0 = 0.01, \lambda = 0.01, \mu = 0.001$。
2). 模型2 传染病发生的中期，感染者较多，感染率较高，治愈率依然较低。设 $i_0 = 0.1, \lambda = 0.1, \mu = 0.001$。
3). 模型3 传染病发生的后期，感染者很多，传播得到有效控制，感染率降低，治愈率也随着医疗水平的提升而升高。设 $i_0 = 0.5, \lambda = 0.01, \mu = 0.1$。

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
from scipy.interpolate import interp1d

# 1. 数据载入
lambda_value = [0.01, 0.1]        # 设置每个感染者每天感染人数，也即感染率
i0_value = [0.01, 0.1, 0.5]       # 设置初始感染者比例
mu_value = [0.002, 0.1]           # 设置治愈率
t1 = np.linspace(0, 1000, 1000)    # 定义时间点数组
t2 = np.linspace(0, 100, 100)    # 定义时间点数组

# 2. 模型定义
# 2.1 传染病发生的初期，感染者较少，感染率较低，治愈率也较低
def SIS(I, t, lamb, mu):
    sigma_value = lamb/mu
    k = 1 - 1/sigma_value
    return lamb * I * (k - I)

# 3. 求解微分方程并输出数值解
# 3.1 使用odeint函数求解微分方程
# 传染病发生的初期，感染者较少，感染率较低，治愈率也较低
solution_SIS1 = odeint(SIS, i0_value[0], t1, args=(lambda_value[0],mu_value[0]))     # 前期
# 传染病发生的中期，感染者较多，感染率较高，治愈率依然较低
solution_SIS2 = odeint(SIS, i0_value[1], t2, args=(lambda_value[1],mu_value[0]))     # 中期
# 传染病发生的后期，感染者较多，传播得到有效控制，感染率降低，治愈率也随着医疗水平的提升而升高
solution_SIS3 = odeint(SIS, i0_value[2], t2, args=(lambda_value[0],mu_value[1]))     # 后期
# 3.2 计算 dI/dt
dI_dt_solution_SIS1 = np.gradient(solution_SIS1[: ,0], t1)            # 前期
dI_dt_solution_SIS2 = np.gradient(solution_SIS2[: ,0], t2)            # 中期
dI_dt_solution_SIS3 = np.gradient(solution_SIS3[: ,0], t2)            # 后期
# 3.3 创建一个插值函数来平滑dI/dt的值
dIdt_SIS1 = interp1d(t1, dI_dt_solution_SIS1, kind='cubic')           # 前期
max_dI_dt_SIS1 = np.max(dI_dt_solution_SIS1)
max_t_SIS1 = t1[np.where(dI_dt_solution_SIS1 == max_dI_dt_SIS1)]
dIdt_SIS2 = interp1d(t2, dI_dt_solution_SIS2, kind='cubic')           # 中期
max_dI_dt_SIS2 = np.max(dI_dt_solution_SIS2)
max_t_SIS2 = t2[np.where(dI_dt_solution_SIS2 == max_dI_dt_SIS2)] 
dIdt_SIS3 = interp1d(t2, dI_dt_solution_SIS3, kind='cubic')           # 后期
max_dI_dt_SIS3 = np.max(dI_dt_solution_SIS3)
max_t_SIS3 = t2[np.where(dI_dt_solution_SIS3 == max_dI_dt_SIS3)]

# 4. 绘制感染率曲线和感染速度曲线
# 4.1 SI模型
plt.figure(figsize=(16, 8))
plt.subplot(2,4,1)
plt.plot(t1, solution_SI)
plt.axhline(y=1.0, color='r', linestyle='--')   # 绘制一条参考线，表示全部人口均被感染
plt.xlabel('time $(t)$')
plt.ylabel('$i(t)$')
plt.title('Infectious (SI)')
plt.subplot(2,4,2)
plt.plot(t1, dI_dt_solution_SI)
plt.plot(max_t_SI, max_dI_dt_SI, 'ob')
plt.text(max_t_SI+40, max_dI_dt_SI, '[' + str(np.round(max_t_SI[0], 2)) + ', ' + str(np.round(max_dI_dt_SI, 4)) + ']')
plt.axvline(x=max_t_SI, color='r', linestyle='--')
plt.xlabel('time $(t)$')
plt.ylabel('Dervative $di(t)/dt$')
plt.title('Infectious rate (SI)')
# 4.2 SIS模型前期
plt.subplot(2,4,3)
plt.plot(t1, solution_SIS1)
plt.axhline(y=1.0, color='r', linestyle='--')   # 绘制一条参考线，表示全部人口均被感染
plt.axhline(y=1-1/(lambda_value[0]/mu_value[0]), color='b', linestyle='--')          # 绘制一条参考线，表示被感染上限
plt.xlabel('time $(t) (\sigma = {:.2f}$)'.format(lambda_value[0]/mu_value[0]))
plt.ylabel('$i(t)$')
plt.title('Infectious (SIS-early)')
plt.subplot(2,4,4)
plt.plot(t1, dI_dt_solution_SIS1)
plt.plot(max_t_SIS1, max_dI_dt_SIS1, 'ob')
plt.text(max_t_SIS1+40, max_dI_dt_SIS1, '[' + str(np.round(max_t_SIS1[0], 2)) + ', ' + str(np.round(max_dI_dt_SIS1, 4)) + ']')
plt.axvline(x=max_t_SIS1, color='r', linestyle='--')   # 绘制一条参考线，表示全部人口均被感染
plt.xlabel('time $(t)$')
plt.ylabel('Dervative $di(t)/dt$')
plt.title('Infectious rate (SIS-early)')
# 4.3 SIS模型中期
plt.subplot(2,4,5)
plt.plot(t2, solution_SIS2)
plt.axhline(y=1.0, color='r', linestyle='--')   # 绘制一条参考线，表示全部人口均被感染
plt.axhline(y=1-1/(lambda_value[1]/mu_value[0]), color='b', linestyle='--')          # 绘制一条参考线，表示被感染上限
plt.xlabel('time $(t) (\sigma = {:.2f}$)'.format(lambda_value[1]/mu_value[0]))
plt.ylabel('$i(t)$')
plt.title('Infectious (SIS-interim)')
plt.subplot(2,4,6)
plt.plot(t2, dI_dt_solution_SIS2)
plt.plot(max_t_SIS2, max_dI_dt_SIS2, 'ob')
plt.text(max_t_SIS2+4, max_dI_dt_SIS2, '[' + str(np.round(max_t_SIS2[0], 2)) + ', ' + str(np.round(max_dI_dt_SIS2, 4)) + ']')
plt.axvline(x=max_t_SIS2, color='r', linestyle='--')   # 绘制一条参考线，表示全部人口均被感染
plt.xlabel('time $(t)$')
plt.ylabel('Dervative $di(t)/dt$')
plt.title('Infectious rate (SIS-interim)')
# 4.4 SIS模型后期
plt.subplot(2,4,7)
plt.plot(t2, solution_SIS3)
plt.axhline(y=1.0, color='r', linestyle='--')   # 绘制一条参考线，表示全部人口均被感染
plt.xlabel('time $(t) (\sigma = {:.2f}$)'.format(lambda_value[0]/mu_value[1]))
plt.ylabel('$i(t)$')
plt.title('Infectious (SIS-late)')
plt.subplot(2,4,8)
plt.plot(t2, dI_dt_solution_SIS3)
plt.plot(max_t_SIS3, max_dI_dt_SIS3, 'ob')
plt.text(max_t_SIS3+4, max_dI_dt_SIS3, '[' + str(np.round(max_t_SIS3[0], 2)) + ', ' + str(np.round(max_dI_dt_SIS3, 4)) + ']')
plt.axvline(x=max_t_SIS3, color='r', linestyle='--')   # 绘制一条参考线，表示全部人口均被感染
plt.xlabel('time $(t)$')
plt.ylabel('Dervative $di(t)/dt$')
plt.title('Infectious rate (SIS-late)')
plt.subplots_adjust(wspace=0.5, hspace=0.3)
plt.show()

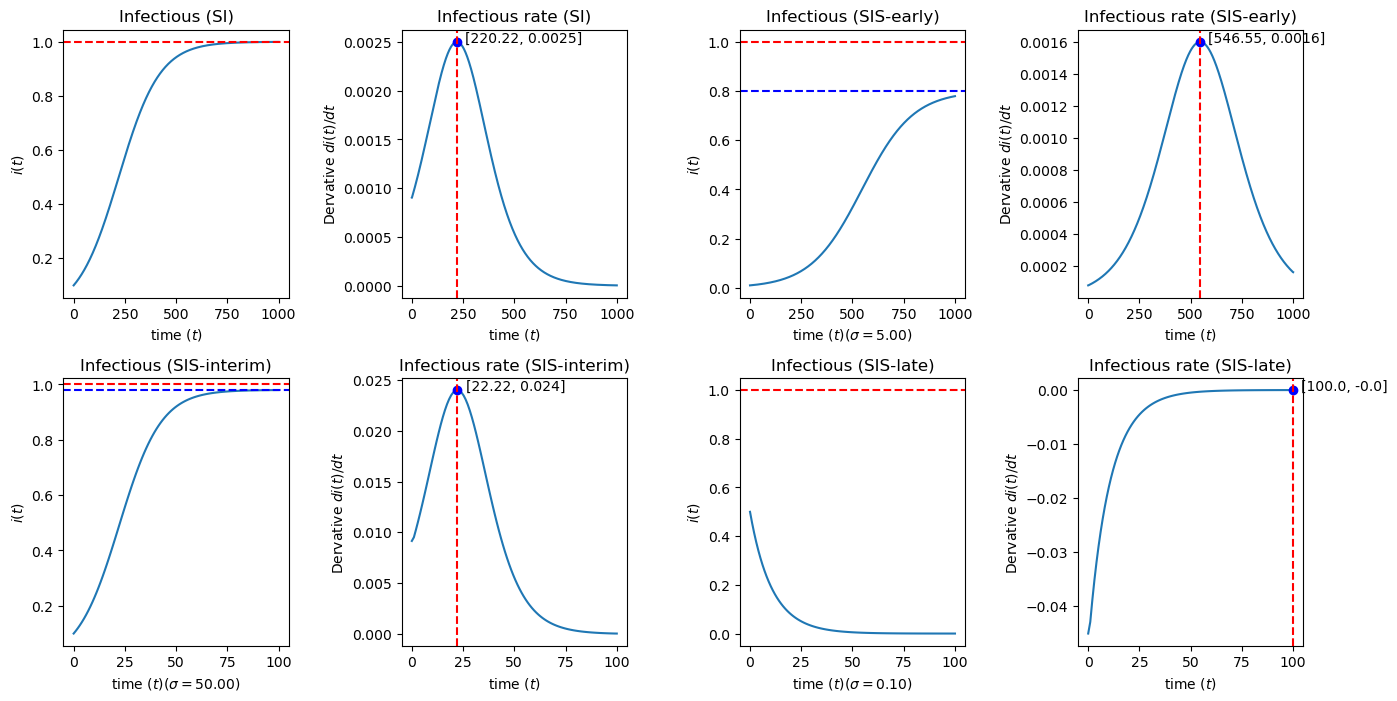
从上面的实验结果来看（图12 v.s 图34），在相同的设定下，SIS模型由于增加了治愈率 $\mu$，所以感染人数的峰值得到了一定的控制，并且高峰时刻从600左右延迟到了1000，并且感染的速度也得到了控制（$0.0025 \rightarrow 0.0016$），且峰值的出现也得到了有效控制。然而，在疫情爆发的中期，由于感染人数（基数）的快速增加，感染率也随着上升时，疫情的爆发呈现不可控状态，几乎和没有治愈率存在的SI模型持平，并且更早地达到峰值（$t=25$)。我们可以发现，在前期和中期的阶段， $\sigma > 1$ 时，微分方程（15）依然是一个 logistic 方程，$i(t)$ 呈S形曲线上升，当 $t \rightarrow \infty$ 时 $i \rightarrow 1-1/\sigma$。当感染率 $\lambda$ 足够大时($>> \mu$)，其呈现的状态于SI模型相似。此时，虽然治愈率可以适当控制峰值人数，但收效甚微，最终大多数人都会被感染。说明，有效控制传染，依然控制疫情爆发最有效的策略。

继续观察实验结果（图78），当 $\sigma \leq 1$，则方程（15）的右端恒为负，曲线$i(t)$将单调下降，当 $t \rightarrow \infty$ 时 $i \rightarrow 0$。也就是说，如果传染率得到有效控制，只要增加治愈能力，疫情的爆发是可以得到有效控制的，最终所有的感染者都会被治愈。

2.4 SIR模型

许多传染病如天花、流感、 麻疹等，治愈后免疫力很强，于是患者愈后不会成为易感染的健康人，当然也不再是感染者。此外，有些传染病的传染性在疫苗的影响下也会大幅降低，因此我们也可以将注射疫苗的人群看做是免疫力很强的人。传染病模型中，我们将病愈免疫后的人、注射疫苗的人，以及因病死亡的人称为治愈者（Recovered），由此将这个模型称为 SIR模型。

2.4.1 基本假设

假设8 人群分为健康者、病人及病愈后具有免疫力而退出系统的治愈者3类。设任意时刻 $t$，这三类人群占人口的比例分别为 $s(t), i(t)$ 和 $r(t)$。
假设9 病人的日感染率为 $\lambda$，日治愈率为 $\mu$，传染强度 $\sigma=\lambda/\mu$。
假设10 人口总数 $N$ 为固定常数，即不包含自然死亡和因病死亡的人。

2.4.2 模型建立

SIS模型 的人群转移规律可以表示为下图：

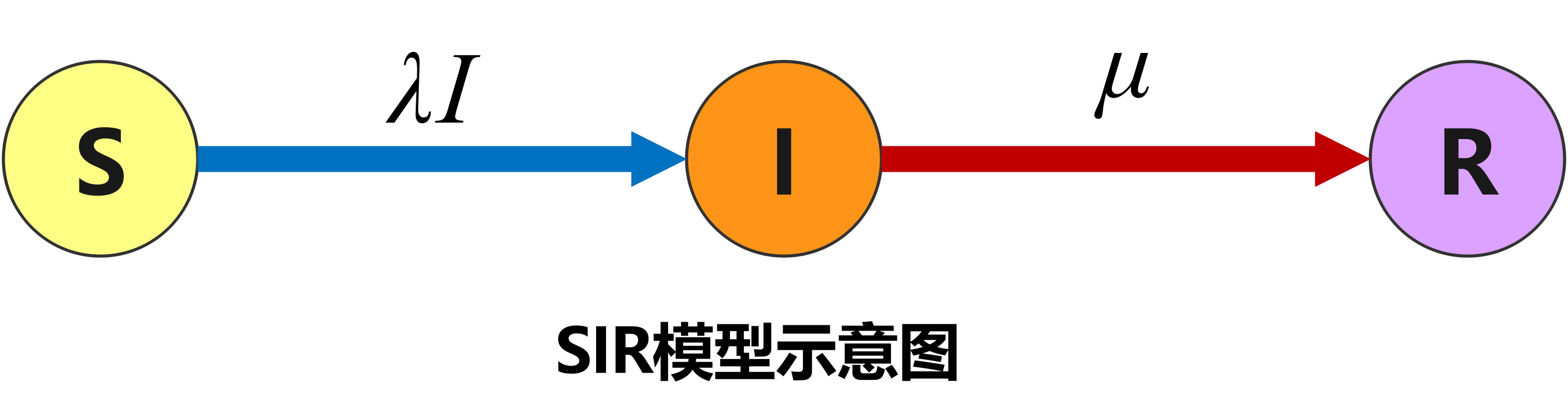
根据假设8可得三类人群的和：

$$s(t) + i(t) + r(t) = 1 \tag{17}$$

关于感染率 $\lambda$、治愈率 $\mu$ 和感染数 $\sigma$ 的假设和定义与SIS模型相同。容易看出，SIS模型中患者比例 $i(t)$ 满足的方程（11）不变，即病人方程为：

$$\frac{di(t)}{dt} = \lambda s (t)i(t) - \mu i(t)$$

但是由于SIR模型中增加了治愈者 $r(t)$，在假设（8）下3个函数 $s(t), i(t)$ 和 $r(t)$ 中有2个独立的，还需要列出健康人 $s(t)$ 或者治愈者 $r(t)$ 的微分方程。根据接触率 $\lambda$ 的假设和定义，$s(t)$ 将单调减少，每天被患者有效接触的健康人数为 $N \lambda s(t) i(t)$，所以健康人方程 $s(t)$ 满足方程（同样约去方程两端的N）：

$$\frac{ds(t)}{dt} = - \lambda s(t)i(t) \tag{18}$$

而治愈者 $r(t)$ 的方程为：

$$\frac{dr(t)}{dt} = \mu i(t) \tag{19}$$

在SIR模型中，容易得到感染者和健康者初始人数分别为 $i(0) = i_0, s(0) = s_0$，治愈者初始人数 $r(0)= 0$。联立方程（11, 18, 19）可得：

$$\begin{cases} \frac{di(t)}{dt} = \lambda s (t)i(t) - \mu i(t)\\ \frac{ds(t)}{dt} = - \lambda s(t)i(t) \\ \frac{dr(t)}{dt} = \mu i(t) \\ i(0) = i_0, s(0) = s_0, r(0)= 0 \end{cases} \tag{20}$$

对于方程组（20）来说，由于存在关系 $s(t) + i(t) + r(t) = 1$，因此，我们可以将方程足进行一定的简化，例如删去$s(t)$ 或者 $r(t)$ 中的一个方程及其对应的初值，此时可以得到简化版的 SIR模型。

$$\begin{cases} \frac{di(t)}{dt} = \lambda s (t)i(t) - \mu i(t) \\\\ \frac{ds(t)}{dt} = - \lambda s(t)i(t) \\\\ i(0) = i_0, s(0) = s_0 \end{cases} \tag{21}$$

以上方程看起来简单，但实际上其无法获得解析解。下面我们使用python来求解它的数值解。

2.4.3 模型求解

与SIS模型类似，我们定义4种模型来分析SIR模型。同时，假设初始治愈者均为0，即 $r(0)= 0$。
1). 模型1 传染病发生的早期A，感染者较少，但病毒的传染性极高，但已经具备了一定的医疗水平。设 $i_0 = 0.01, \lambda = 0.6, \mu = 0.3$。
2). 模型2 传染病发生的早期B，感染者数量和模型1相同，也比较少，病毒的传染性依然极高，而医疗水平也有一定的提高。设 $i_0 = 0.01, \lambda = 0.6, \mu = 0.4$。
3). 模型3 传染病发生的中期，感染者大幅增加，传播得到有效控制，感染率降低，医疗水平依然保持较高水平。设 $i_0 = 0.5, \lambda = 0.1, \mu = 0.4$。
4). 模型4 整体定义和模型3相同，但假设有0.2的人群注射了疫苗。设 $i_0 = 0.5, \lambda = 0.1, \mu = 0.4,$ vaccine $= 0.2$。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint 

# 1. 数据载入
lambda_value = [0.6, 0.6, 0.1, 0.1]       # 设置每个感染者每天感染人数，也即感染率
mu_value = [0.3, 0.4, 0.4, 0.4]           # 设置治愈率
sigma_value = np.array(lambda_value)/np.array(mu_value)  # 计算感染数
i0_value = [0.01, 0.01, 0.5, 0.5]         # 设置初始感染者比例
r0_value = 0                         # 治愈者初始比例为0
vaccine = 0.2                        # 设置疫苗覆盖率
t = np.linspace(0, 60, 60)           # 定义时间点数组

# 2. 模型定义
def SIR(y, t, lamb, mu):
    s, i, r = y
    dsdt = -lamb * s * i
    didt = lamb * s * i - mu * i
    drdt = mu * i
    return [dsdt, didt, drdt]  

# 3. 求解微分方程并进行可视化输出
def SIR_solution(i):
    if i == 3:
        s0_value = 1 - r0_value - i0_value[i] - vaccine
    else:
        s0_value = 1 - r0_value - i0_value[i]  # 计算健康者初始比例
    init = [s0_value, i0_value[i], r0_value]   # 设置初始条件
    solution_SIR = odeint(SIR, init, t, args=(lambda_value[i], mu_value[i]))  # 求解微分方程
    st = solution_SIR[:, 0]                    # 输出解中的健康者比例s(t)
    it = solution_SIR[:, 1]                    # 输出解中的感染者比例i(t)
    rt = solution_SIR[:, 2]                    # 输出解中的治愈者比例r(t)
    
    max_it = np.max(it)
    max_t = t[np.where(it == max_it)]
    plt.subplot(2,4,i+1)                       # 设置子图
    plt.plot(t, st, label='Susceptible')       # 绘制健康者比例s(t)曲线
    plt.plot(t, it, label='Infected')          # 绘制感染者比例i(t)曲线
    plt.plot(t, rt, label='Recovered')         # 绘制治愈者比例r(t)曲线
    plt.plot(max_t, max_it, 'bo')
    plt.vlines(max_t, 0, max_it, colors='b', linestyles='--')
    if i == 3:
        plt.hlines(vaccine, 0, 60, colors='red', linestyles='dashed', label='Vaccine')
    plt.xlabel('Time')                         # 设置x轴标签
    plt.ylabel('Proportion')                   # 设置y轴标签
    plt.ylim(0, 1.0)
    plt.title('SIR model over time ($\sigma=$ {:.2f})'.format(sigma_value[i]))
    plt.legend(loc='upper right')              # 设置图例位置
    plt.grid(True)                             # 显示网格

    
    max_it_st = st[np.where(it == max_it)]
    plt.subplot(2,4, i+5)
    plt.plot(st, it)
    plt.plot(max_it_st, max_it, 'ro')
    plt.vlines(max_it_st, 0, max_it, colors='b', linestyles='--')
    plt.xlabel('$s(t)$')
    plt.ylabel('$i(t)$')
    plt.title('Spread Curve ($s_0 = {:.2f}, 1/\sigma=$ {:.2f})'.format(s0_value, 1/sigma_value[i]))
    if i == 2 or i == 3:
        plt.xlim(0.6, 0.2)
    plt.grid(True)

# 4. 主函数：调用预定义好的函数进行模型求解
plt.figure(figsize=(18, 6))
for i in range(4):
    SIR_solution(i)
plt.subplots_adjust(wspace=0.3, hspace=0.4)
plt.show()

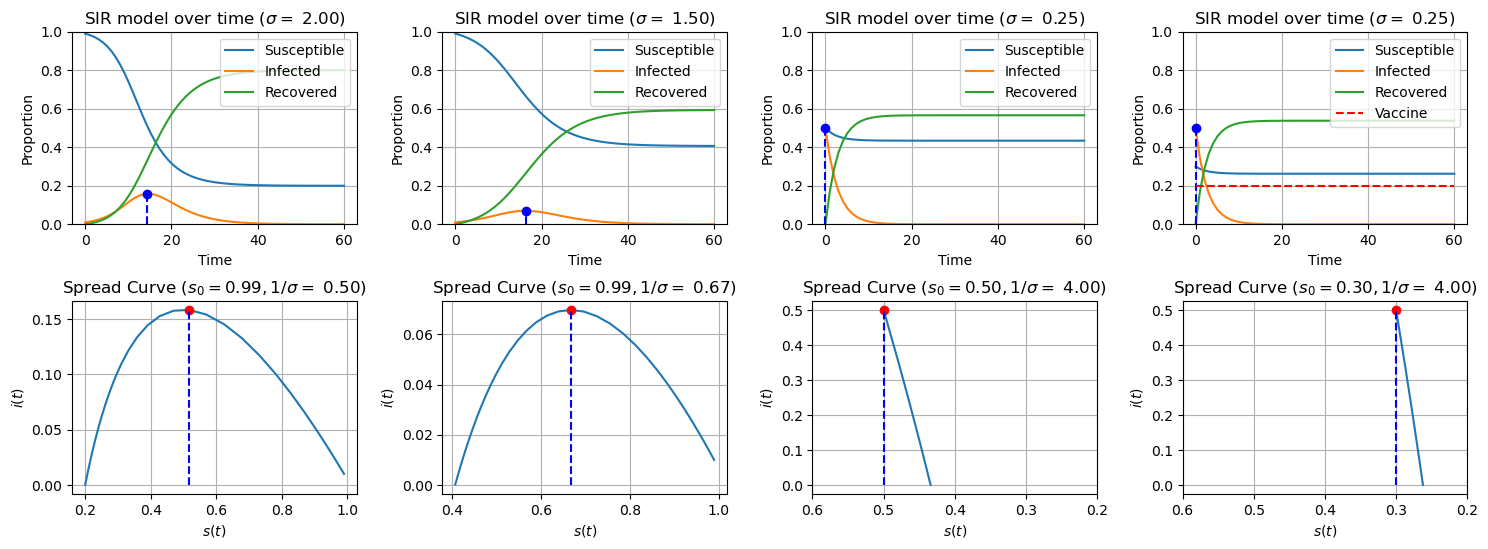
2.4.4 结果分析与评价

由以上结果（图1-4）可以得到以下结论：

1. 健康人比例 $s(t)$ 始终呈单调递减趋势，治愈者比例 $r(t)$ 单调增加，并且最后都趋向稳定值。
2. 在初期（图1，2）中，感染者比例 $i(t)$ 呈S形曲线，主要原因是感染率 $\lambda$ 大于治愈率 $\mu$，也即感染人数 $\sigma > 1$；不过，由于医疗水平的提高，治愈率得到了提高（$(\mu_2=0.4) > (\mu_1=0.3)$，因此感染者的比例得到了有效的控制，同时后者中从未被感染过的人群 $s(t)$ 也远高于前者。
3. 在中期（图3，4）中，初始感染人数 $i(t)=0.5$ 大幅上升，医疗水平相比模型2并没有提高，但由于采取了一定的措施（例如隔离感染者），感染者人群得到了迅速的控制（$i(t) \rightarrow 0$）。
4. 无论是在哪种设定下，感染者比例 $i(t)$ 最终都趋向于 0。当 $t \rightarrow \infty$ 时，$s(t)$ 的稳定值表示在传染病传播过程中最终都没有被感染的人数比例，$i(t)$ 的最大点和最大值表示传染病高潮（感染者最多）到来的时刻和人数比例，这些数值可以衡量传染病传播的强度和速度。
5. 图4给出了注射疫苗后的四类人群曲线，我们发现治愈者并没有明显下降，这意味着部分人群进行疫苗注射并不能够完全控制疫情，对于未注射过疫苗的人群依然有被感染的风险，除非整个感染者人群都被控制（在隔离期中被治愈）。换句话说，为了彻底控制疫情，疫苗的覆盖率必须达到100%；或者通过加强医疗水平，尽快实现感染者的清零。

感染率 $\lambda$ 和治愈率 $\mu$（可以假定死亡率很低）是影响传播过程的重要参数。社会的卫生水平越高感染率 $\lambda$ 越小，医疗水平越高治愈率 $\mu$ 越大，于是感染数 $\sigma (=\lambda / \mu)$ 越小，应该有助于控制传染病的传播。对于不同 $\sigma$ 下的 图1（$\sigma=2.00$）和（图2 $\sigma=1.50$），后者的健康人比例 $s(t)$ 更大，感染者比例 $i(t)$ 更小。

进一步研究表明（图5-8）：

1. 当 $s_0 > 1/\sigma$ 时，$i(t)$ 先增后减，可认为传染病有一个蔓延过程；而若 $s_0 < 1/\sigma$ 时，$i(t)$ 单调减少直至0，表示传染病不会蔓延开来。一般情况下，$i(0)$ 和 $r(0)$ 都很小，$s(0)$ 接近 $1$，所以控制传染病蔓延需要 $\sigma$ 小于 $1$，这可以通过提高卫生水平和医疗水平达到。
2. 控制传染病蔓延的另一途径是降低 $s(0)$，这可以通过提高 $r(0)$，即预防接种使群体免疫来实现。

SIR模型 是一个较典型的系统动力学模型，其突出特点是模型形式为关于多个相互关联的系统变量之间的常微分方程组。类似的建模问题有很多，如河流中水体各类污染物的耗氧、复养、反应、迁移、迁移、吸附、沉降等，食物在人体中的分解、吸收、排泄，污水处理过程中污染物的讲解，微生物、细菌增长或衰减等。这些问题很难求得解析解，可以使用软件求数值解。

三、舱室模型

以上三个传染病模型（SI、SIS、SIR）体现了建模过程的不断深化。SI模型 描述了传染病的蔓延，但不符合实际；SIS和SIR模型则针对愈后是否免疫这两种情况，描述了传播过程，得到患者比例的变化规律。其中 SIR模型 特别值得注意，它是研究更复杂、更实用的许多传染病模型的基础。下面我们再简单介绍几个传染病模型，这些模型都以 SIR模型为基础。在介绍这些模式前，我们先引入一类问题的定义和思考方式，即 舱室模型。

4.1 舱室模型

舱室模型 是流行病学中的一大类模型，它指将人群或系统中的个体或部分个体或系统变量分成若干个舱室，然后分别建立模型来描述这些舱室之间的相互作用和转移关系。通过数学模型语言来描述整个系统，最终将得到一个微分方程组模型。该微分方程组通常是没有解析解的，需要使用Python编程来进行数值求解。

前面介绍过的 SIR模型 是舱室传染病模型的基础，通过进一步考虑更复杂的人群划分和转移可以得到更全面和完善的模型。例如，考虑出生率、死亡率、防疫措施的作用、潜伏期、抵抗能力、考虑地域传播、考虑传播途径（接触、空气、昆虫、水源等）等可以得到不同的舱室模型，例如：

• SEIS模型：易感染者-暴露者-感染者-不免疫者
• SEIR模型：易感染者-暴露者-感染者-治愈者（免疫者）
• SIRS模型：易感染者-感染者-短时免疫者-易感染者

4.2 基于舱室模型的SIR模型

下面我们以 舱室模型 的思想来回顾一下 SIR模型，并讨论如何从舱室转移关系图迁移到微分方程模型组。

前面我们已经给出了 SIS模型 的舱室转移关系图：

在上图中，每个舱室代表一类人群的占比，也对应于一个未知函数，箭头及标签表示舱室间的转移关系和转移速率。对于每个舱室我们都可以建立一个微分方程来描述其变化规律。等式的左边使用导数来表示人群的变化速度，等式的右边表示舱室间的转移量，其中出箭头都是“减”，入箭头都是“加”，对于每一项来说都存在转移人数=转移率×各自舱室人数（各舱室的函数）。对于每个流量来说，要注意整体流量的平衡，即对于流量 $\alpha$，流出舱室A的量应该等于流入舱室B的量。由此，可以分别得到 SIR模型 关于感染者 $i(t)$、易感染者 $s(t)$和治愈者 $r(t)$ 的三个微分方程如下：

$$\begin{cases} \frac{di(t)}{dt} = \lambda s (t)i(t) - \mu i(t) & (1) \\\\ \frac{ds(t)}{dt} = - \lambda s(t)i(t) & (2)\\\\ \frac{dr(t)}{dt} = \mu i(t) & (3) \end{cases} \tag{20}$$

从以上微分方程组，我们可以得到以下结论：

1. 对于易感染人群 $s(t)$，其入流量为0，出流量为新增被感染人群，即 $\lambda s(t) i(t)$；
2. 对于感染者人群 $i(t)$，其入流量和易感染人群的出流量一致，都是新增的被感染人群 $\lambda s(t) i(t)$，其出流量等于新增被治愈的人，即 $\mu i(t)$；
3. 对于治愈者人去 $r(t)$，入流量等于感染者人群的出流量 $\mu i(t)$，没有出流量。

此外，由于总流量是平衡的，即存在 $i(t) + s(t) + r(t) = 1$，因此在进行数值求解时，可以认为有一个微分方程是多余的（可以由其他微分方程来表示）。

在建立复杂的传染病模型时，我们可以先绘制出舱室转移关系图，然后再根据上述规律来建立微分方程组，最后利用Python的 odeint() 函数来进行数值求解即可。

4.3 SEIR模型

在 SIR 模型的基础上，将已感染但处于潜伏期的人群称为暴露者 E，也考虑到模型中，即成为 SEIR 模型。该模型包含易感者、暴露者、感染者、移出者四类人群，适合有潜伏期且治愈后获得终身免疫的传染病，如带状疱疹等。首先先绘制舱室转移关系图如下：

根据上图，易感者 $S$ 先以 $\lambda I$ 的速度转移到暴露类 $E$，再以$\gamma$ 的速度转移到感染类 $I$，最后再以 $\mu$ 的速度转移到移出类 $R$。再按前面介绍的规律可以写出微分方程组，并赋予一定的初值可得：

$$\begin{cases} \frac{ds(i)}{dt} = -\lambda i(t) s(t) \\ \frac{de(i)}{dt} = \lambda i(t) s(t) - \gamma e(t) \\ \frac{di(t)}{dt} = \gamma e(t) - \mu i(t) \\ \frac{dr(t)}{dt} = \mu i(t) \\ s(0) = s_0, e(0) = e_0, i(0) = i_0, r(0) = 0 \end{cases}\tag{22}$$

根据 $s(t) + e(t) + i(t) + r(t) =1$ 和流量平衡原则，可以去掉其中一个微分方程再进行数值求解（为了方便解释，也可不进行去除，而是在计算中灵活使用）。但应知晓两种方法得出的结果是一致的。有一个微分方程是多余的，去掉最后一个，得到如下 SEIR 模型：

$$\begin{cases} \frac{ds(i)}{dt} = -\lambda i(t) s(t) \\ \frac{de(i)}{dt} = \lambda i(t) s(t) - \gamma e(t) \\ \frac{di(t)}{dt} = \gamma e(t) - \mu i(t) \\ s(0) = s_0, e(0) = e_0, i(0) = i_0 \end{cases}\tag{22}$$

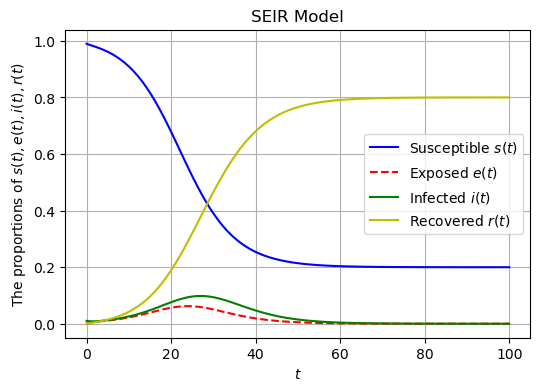
下面我们给出 SEIR模型 的数值求解代码，并绘制出四类人群的变化曲线图。假设 $i_0 = 0.01, r_0 = e_0 = 0, \lambda = 0.6, \gamma = 0.5, \mu = 0.3$。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint 

# 1. 数据载入
lambda_value = 0.6                # 设置每个感染者每天感染人数，也即感染率
mu_value = 0.3                    # 设置治愈率
gamma_value = 0.5                 # 设置潜伏期后感染的比例
i0_value = 0.01                   # 设置感染者初始比例
r0_value = 0                      # 设置治愈者初始比例为0
e0_value = 0                      # 设置暴露者初始比例为0
s0_value = 1 - r0_value - i0_value - e0_value
t = np.linspace(0, 100, 100)      # 定义时间点数组

# 2. 模型定义
def SEIR(y, t, lamb, gamma, mu):
    s, e, i = y
    dsdt = -lamb * s * i
    dedt = lamb * s * i - gamma * e
    didt = gamma * e - mu * i
    return [dsdt, dedt, didt]  

# 3. 求解微分方程
init = [s0_value, e0_value, i0_value]
solution_SEIR = odeint(SEIR, init, t, args=(lambda_value, gamma_value, mu_value))
st = solution_SEIR[:, 0]                    # 输出解中的健康者比例s(t)
et = solution_SEIR[:, 1]                    # 输出解中的暴露者比例e(t)
it = solution_SEIR[:, 2]                    # 输出解中的感染者比例i(t)
rt = 1 - st - et - it                       # 利用平衡原则计算治愈者比例r(t)                    # 输出解中的治愈者比例r(t)

# 4. 可视化输出曲线
plt.figure(figsize=(6, 4))
plt.plot(t, st, 'b', label='Susceptible $s(t)$')
plt.plot(t, et, 'r--', label='Exposed $e(t)$')
plt.plot(t, it, 'g', label='Infected $i(t)$')
plt.plot(t, rt, 'y', label='Recovered $r(t)$')
plt.xlabel('$t$')
plt.ylabel('The proportions of $s(t), e(t), i(t), r(t)$')
plt.title('SEIR Model')
plt.legend(loc='best')
plt.grid(True)
plt.show()

在以上所有模型的定义中，我们都假定感染率参数 $\lambda$ 和治愈率参数 $\mu$ 是常数，而在实际的传播过程中，这种假设并不一定准确，这两个参数都会随着预防措施的加强与医疗水平的提高而发生较大变化。此外，还有很多没有考虑的因素，如人口的出生与死亡，迁入和迁出等，还可以考虑更细致的因素， 如人群流动速度、易感人群的年龄分布、不同人群对疾病的易感性，患病者的症状轻重，人口密度，医疗卫生程度，检验检疫手段，政府重视程度，隔离措施、人群心理因素等。这些因素都对暴露数、发病率、治愈率、传染期长度有着直接或间接的影响。

在第四小节中，我们将讨论情况更加复杂的情况SARS的传播。

四、SARS的传播

2003年SARS在我国爆发初期，限于卫生部门和公众对这种疾病的认识，使其处于几乎不受制约的自然传播形式，后期随着卫生部门预防和治疗手段的不断加大，SARS的传播受到严格控制。虽然影响这个过程的因素众多，也不只有健康人、患者、移除者3个人群，但是仍然可以用愈后免疫的SIR模型来描述。并且，越复杂的模型包含的参数越多，为确定这些参数所需要的疫情数据就越全面，而实际上能够得到的数据是有限的。

4.1 问题提出（回顾）

2002年冬到2003年春，一种名为SARS（severe acute respiratory syndrome, 严重急性呼吸道综合症，民间俗称非典）的传染病肆虐全球。SARS首发于中国广东，迅速扩散到东南亚乃至30多个国家和地区，包括医务人员在内的多名患者死亡，引起社会恐慌、媒体关注以及各国政府和联合国、世界卫生组织的高度重视、积极应对，直至最终疫情的蔓延。突如其来的SARS及其迅猛的传播和严重的后果，成为21世纪的第一大社会热点事件。

SARS被控制住不久，2003年的全国大学生数学建模竞赛就以“SARS传播”命名当年的A题和C题，题目中要求“建立你们自己的模型；特别要说明怎样才真正预测以及能为预防和控制提供可靠、足够的信息的模型，这样做的困难是哪里？对于卫生部门所采取的措施做出评论，如：提前或延后5天采取严格隔离措施，对疫情传播所造成的影响做出估计。”题目还给出了北京市从2003年4月20日至6月23日逐日的疫情数据供参考（表1 是部分数据）。

表1 北京市的疫情数据 数据文件：Project03_SARS的传播。

日期	已确诊病例累计	现有疑似病例	死亡累计	治愈出院累计
4月20日	339	402	18	33
4月21日	482	610	25	43
4月22日	588	666	28	46
$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$
6月22日	2521	2	191	2257
6月23日	2521	2	191	2277

本教案先介绍数学、医学领域中基本的传染病模型，然后结合赛题，介绍几个描述、分析SARS传播过程的模型及求解结果。这些模型对于COVID-19新冠肺炎的传播与预测也同样适用。

4.2 模型一：参数时变的SIR模型

4.2.1 模型构造

为了计算的方便，假设总人数不变且恒定为 $S$。使用 $s(t), i(t), r(t)$ 分别表示第 $t$ 天健康人、感染者、移除者（治愈与死亡之和）的数量（不再是比值），$\lambda(t), \mu(t)$ 分别表示第 $t$ 天的感染率和移除率（治愈率与死亡率之和），注意此处的 $\lambda(t), \mu(t)$ 都是以时间 $t$ 为变量的函数，不再是定值。此外，在前面的模型中，我们使用 $r(t)$ 表示治愈者，而在这里我们使用 $r(t)$ 表示移除者，也就是说 $r(t)$ 表示的是治愈者与死亡者的总和。

结合前面小节的分析，我们可以将 SIR模型 表示为如下参数时变方程：

$$\begin{cases} \frac{di(t)}{dt} = \lambda(t) s(t)i(t) - \mu i(t) & (1) \\\\ \frac{ds(t)}{dt} = - \lambda(t) s(t)i(t) & (2)\\\\ \frac{dr(t)}{dt} = \mu(t) i(t) & (3) \end{cases} \tag{23}$$

由于总人数 $S$ 几乎是常数，且远大于 $i$ 和 $r$，所以可以忽略 $s(t)$ 对 $i(t)$ 和 $r(t)$ 的影响，得到如下简化模型：

$$\begin{cases} \frac{di(t)}{dt} = \lambda(t) i(t) - \mu(t) i(t) \\\\ \frac{dr(t)}{dt} = \mu(t) i(t) \end{cases} \tag{24}$$

下面用微分方程组（23）研究SARS传播。

4.2.2 数据载入及预处理

在本例中，我们首先载入赛题提供的数据文件 数据文件Project03_SARS的传播。

针对数据文件中的数据，建议先进行可视化并进行分析和预处理，此处我们使用 pandas 工具包中的 read_excel() 函数来读取数据 .xlsx 文件。

import pandas as pd

data_pd = pd.read_excel('../../Data/Project03/SARS.xlsx')
data_pd

从上表给出的数据中，我们可以得到以下信息：

• 数据表格本身包含的日期星期为 "xx月xx日"，但因数据格式的问题导致其转换为了整数。但对于本例来说，我们并不需要这个信息。考虑到模型中需要顺序的时间序列 $t$ 标识数据，因此可以考虑通过数据的行数来手动生成时间序列。例如：np.arange(0, len(data), 1) 可以生成一个从 $t=0$ 开始，到$t=n-1$ 的时间序列。
• 第4列 死亡累计 和第5列 治愈出院累计 之和为本例的 移除者，即 r(t)。
• 第2列 已确诊病例累计 减去移除者 r(t) 是当前感染者数量，即 i(t)。
• 从原始数据中可看出，在 $t=25$（天）左右SARS的传播达到高潮（感染者最多）。

根据以上分析，我们首先将原始数据进行可视化，得到如下结果：

import numpy as np
import matplotlib.pyplot as plt

data = data_pd.values               # 将pandas数据转换为numpy数组
t = np.arange(0, len(data), 1)
R = data[:, 3] + data[:, 4]         # 治愈者 = 治愈者+死亡者
I = data[:, 1] - R                  # 感染者 = 确诊患者-死亡者-治愈者

plt.figure(figsize=(10, 4))
plt.subplot(1,2,1)
plt.scatter(t, I, s=5, label='Recovered $r(t)$')
plt.xlabel('Time $t$ = [2003-04-20 ~ 2003-06-23]')
plt.ylabel('$i(t)$')
plt.title('Infestor Curve')
plt.grid(True)
plt.subplot(1,2,2)
plt.scatter(t, R, s=5, label='Infected $i(t)$')
plt.xlabel('Time $t$ = [2003-04-20 ~ 2003-06-23]')
plt.ylabel('$r(t)$')
plt.title('Recovered Curve$')
plt.grid(True)
plt.show()

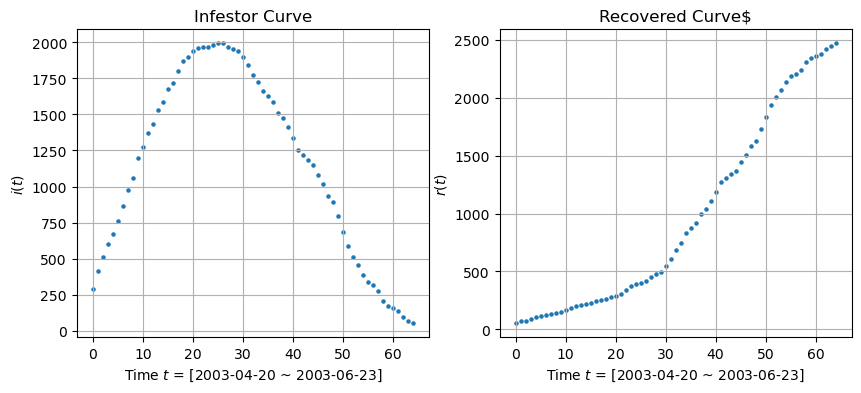
4.2.3 参数估计与拟合

为了求解微分方程，给出感染者和移除者的数值解和可视化曲线，我们首先需要对时变感染率和移除率进行估计。此处，可以考虑取 $r(t), i(t)$ 的差分 $\Delta r(t), \Delta i(t)$ 作为方程组 (24) 左端导数的近似值。于是，可以得到

$$\mu(t) = \frac{\Delta r(t)}{i(t)} \tag{25.1}$$

代入 (24) 得到

$$\lambda(t) = \frac{\Delta i(t) + \Delta r(t)}{i(t)} \tag{25.2}$$

需要注意的是，在上述的差分运算中 $\Delta i(t) = i(t) - i(t-1) , \Delta r(t) = r(t) - r(t-1)$。

下面的代码给出了对参数 $\lambda(t), \mu(t)$ 的散点图。从图形来看，大体上像是 指数曲线（估测），但也可以考虑使用 高次多项式曲线 来进行拟合。在本例中，我们使用后者，有兴趣的读者可以考虑使用 指数曲线 来对散点图进行拟合，得到的结果与 高次多项式曲线 相差不大，但略优于多项式曲线。

PS：在使用指数曲线进行拟合的时候，需要注意指数曲线的参数 $\lambda(t)$ 的取值范围，如果 $\lambda(t) < 0$，则指数曲线将无法拟合数据。此时，可以考虑只对部分数据进行拟合。例如，对于 $\lambda(t)$ 可以考虑使用前20天的数据进行拟合，对于 $\mu(t)$ 可以考虑使用第20~50天的数据进行拟合。

import numpy as np
import matplotlib.pyplot as plt

# 1. 计算感染率和移除率的差分
lamb_delta = (np.diff(I) + np.diff(R)) / I[1::]    # 计算感染率的差分
mu_delta = np.diff(R) / I[1::]                     # 计算移除率的差分
t_delta = t[0:-1]                                  # 根据差分的特性移除最后一个时间点

# 2. 使用高次多项式曲线对已知数据进行拟合
coef_lamb = np.polyfit(t_delta, lamb_delta, deg=4) # 使用4次多项式拟合感染率
coef_mu = np.polyfit(t_delta, mu_delta, deg=4)     # 使用4次多项式拟合移除率

# 3. 根据拟合系数计算感染率和移除率
lamb_hat = np.polyval(coef_lamb, t)                  # 使用拟合的参数预测感染率
mu_hat = np.polyval(coef_mu, t)                      # 使用拟合的参数预测移除率

# 4. 可视化已知数据的散点及使用拟合函数预测的曲线
plt.figure(figsize=(10, 4))
plt.subplot(1,2,1)
plt.scatter(t_delta, lamb_delta, s=5, label='lambda')
plt.plot(t, lamb_hat, 'b')
plt.xlabel('$t$')
plt.ylabel('$\lambda(t)$')
plt.title('Infection rate $\lambda (t)$')
plt.grid(True)
plt.subplot(1,2,2)
plt.scatter(t_delta, mu_delta, s=5, label='mu')
plt.plot(t, mu_hat, 'b')
plt.xlabel('$t$')
plt.ylabel('$\mu(t)$')
plt.title('Recovery rate $\mu (t)$')
plt.grid(True)
plt.show()

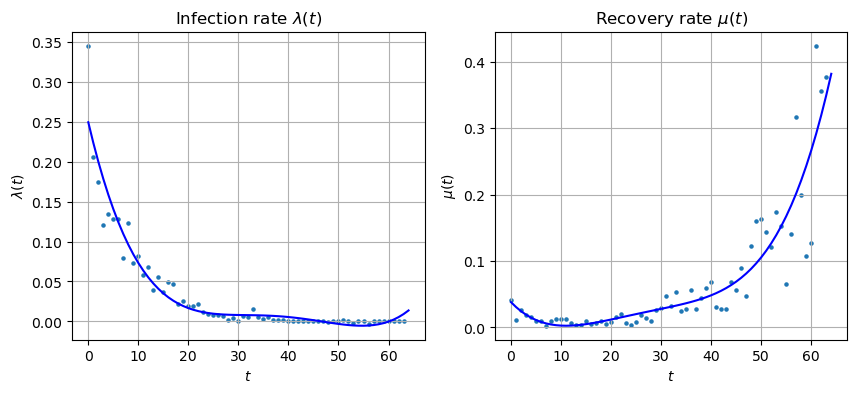
从上图中的曲线和散点对比来看，四次多项式拟合的效果还是比较理想的。根据拟合曲线，我们可以发现，感染率从一开始就迅速下降，到 $t=15$（天）以后已经很小，说明疫情传播受到有力制约：移除率在 $t=50$（天）之前变化不大，以后较快上升，表明经过约1个月（50-15 天）的治疗期后，传播达到高潮时的大量患者被治愈。

4.2.4 模型求解与检验

进一步将拟合得到的 $\hat{\lambda} (t)$ 和 $\hat{\mu} (t)$ 代入微分方程（24）并求解之，我们可以得到方程组的数值解。结果显示，与 $i(t), r(t)$ 的原始数据（图中圆点）比较，$i(t)$ 的计算值整体偏小，$r(t)$ 的结果也有类似的情况，说明在模型构造、参数拟合等方面仍需改进。

• 绘制真实值和预测值之间的对比曲线

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签

# 2. 模型定义
def SIR(y, t, lamb_t, mu_t):
    i, r = y
    didt = lamb_t(t) * i - mu_t(t) * i
    drdt = mu_t(t) * i
    return [didt, drdt]

def lambda_func(t):
    return np.polyval(coef_lamb, t)

def mu_func(t):
    return np.polyval(coef_mu, t)

y0 = [I[0], R[0]]
res = odeint(SIR, y0, t, args=(lambda_func, mu_func))
it = res[:, 0]
rt = res[:, 1]

plt.figure(figsize=(10, 4))
plt.subplot(1,2,1)
plt.scatter(t, I, s=5, label='真实值')
plt.plot(t, it, 'b', label='预测值')
plt.xlabel('Time $t$ = [2003-04-20 ~ 2003-06-23]')
plt.ylabel('i(t)')
plt.title('感染人数曲线')
plt.legend(loc='best')
plt.grid(True)
plt.subplot(1,2,2)
plt.scatter(t, R, s=5, label='真实值')
plt.plot(t, rt, 'b', label='预测值')
plt.xlabel('Time $t$ = [2003-04-20 ~ 2003-06-23]')
plt.xlabel('Time $t$ = [2003-04-20 ~ 2003-06-23]')
plt.ylabel('r(t)')
plt.title('移除者曲线')
plt.legend(loc='best')
plt.grid(True)
plt.show()

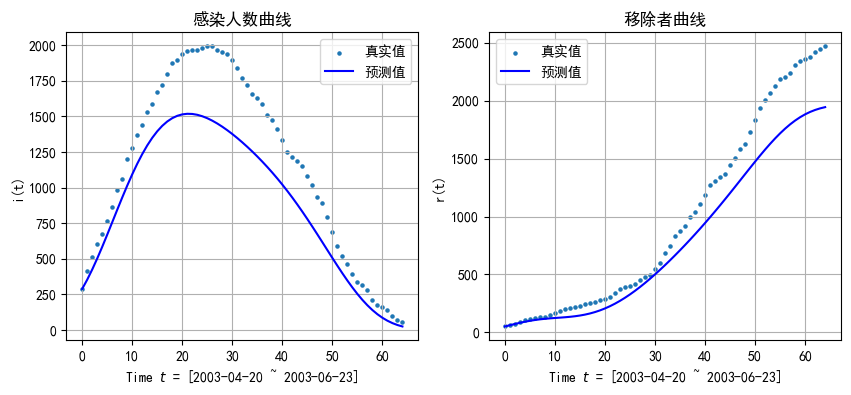
• 计算真实值和预测值之间的标准差

diff_I = I - it
diff_R = R - rt

std_I = np.std(diff_I)
std_R = np.std(diff_R)

print('I 和 it 的标准差: {:.2f}'.format(std_I))
print('R 和 rt 的标准差: {:.2f}'.format(std_R))

I 和 it 的标准差: 157.48
R 和 rt 的标准差: 167.18

4.3 模型二：引入不可控带菌者和疑似已感染者的模型

该模型为SARS传播过程中受到严格控制条件下的模型。在该模型中，$s(t), i(t), r(t), \mu$ 的含义与SIR模型相同。此外，在该模型中新增加两个人群：不可控带菌者和疑似已感染者，其比例分别记作 $c(t)$ 和 $e(t)$。每个不可控带菌者发病后（收治前）每天有效感染的人数为 $\lambda$（相当于SIR模型的感染率），$\lambda$ 中可以控制的比例为 $\alpha$，不可控带菌者每天转化为已感染者的比例为 $\epsilon$。疑似已感染者每天被排除的比例为 $\beta$，每天被确诊的比例为 $\gamma$。5个人群之间的转移关系如下图所示。

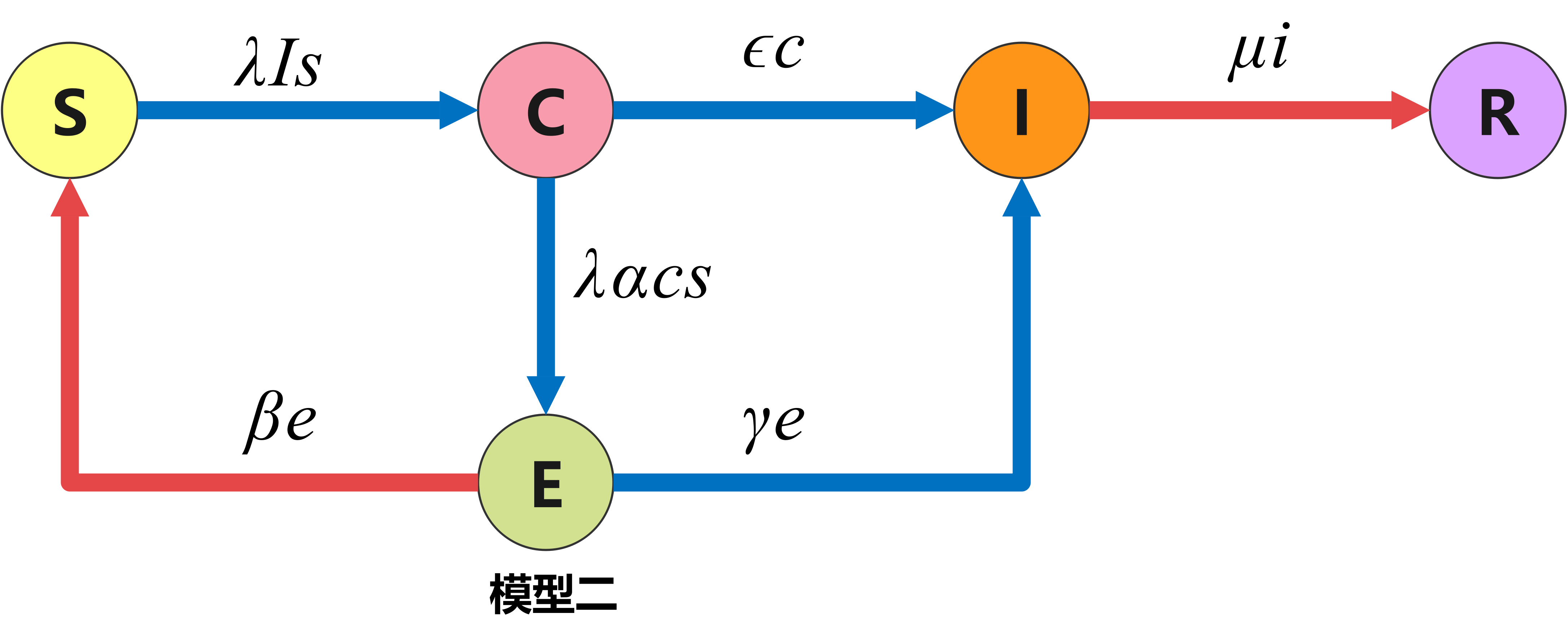
仿照SIR模型并按照上图的转移关系可建立如下方程：

$$\begin{cases} s(t) + c(t) + e(t) + i(t) + r(t) = 1 \\ \frac{ds(t)}{dt} = \beta e(t) - \lambda cs \\ \frac{dc(t)}{dt} = \lambda (1 - \alpha) cs - \epsilon c \\ \frac{de(t)}{dt} = -(\beta + \gamma) e + \lambda \alpha cs \\ \frac{di(t)}{dt} = \epsilon c - \mu i + \gamma e \\ \frac{dr(t)}{dt} = \mu i \end{cases} \tag{26}$$

当参数 $\lambda, \mu, \epsilon, \alpha, \beta, \gamma$ 确定后，由方程组（26）中的任意5个方程及初值 $s(0), i(0), c(0), e(0), r(0)$ 中任意4个，可以计算传播过程中5类人群的比例 $s(t), c(t), e(t), i(t)$ 和 $r(t)$。

这个模型中各个参数的估计可通过两种方式进行，一种是直接利用实际数据做出估计（如模型一），另一种是先由经验估计的初值，代入模型计算，再根据计算值与实际值的偏差调整估计值。

4.4 模型三：引入尚未隔离和已经隔离已感染者的模型

（本节资料来源：姜启源, 谢金星, 叶俊 《数学模型（第五版）》）

下面再介绍一个关于SARS在中国的传播与控制的模型。

[1] Zhou Y, Ma Z, Brauer F. A Discrete Epidemic Model for SARS Transmission and Control in China. Mathematical and Computer Modelling, 2004, 40:1491-1506.

我们结合下图说明各个人群的构造和转移关系（图中没有画出易感染者 $S(t)$）。

• $E(t)$ 表示处于潜伏期的易感染者，有弱传染性
• $I(t)$ 表示已发病但尚未隔离的已感染者，有强传染性
• $Q(t)$ 表示已发病且已隔离、尚未治疗的已感染者（无传染性）
• $J(t)$ 表示已发病且已隔离、正在治疗的已感染者（无传染性）
• $R(t)$ 表示治愈者（无传染性、有免疫性）
• $\beta (t)$ 表示感染率，每个有强传染性的已感染者每天传染的人数
• $k$ 表示一个处于潜伏期（E）的已感染者转变成成未隔离（I）的已感染者的分值，也即传染性。
• $\epsilon, \lambda$ 表示处于潜伏期（E）的已感染者分别转入未隔离（I）和已隔离（Q）的已感染者的比例
• $\theta, \sigma$ 表示未隔离（I）和已经隔离（Q）的已感染者分别转入正在治疗（J）的人群的比例
• $\gamma$ 表示正在治疗的已感染者（J）治愈的比例
• $\delta$ 表示未隔离（I）和正在治疗（J）的已感染者的死亡率

按照上图各个人群的转移关系建立如下方程：

$$\begin{cases} \frac{dE}{dt} = \beta(t)(kE+I) - (\epsilon + \lambda)E \\ \frac{dI}{dt} = \epsilon E - (\theta + \delta) I \\ \frac{dQ}{dt} = \lambda E - \sigma Q \\ \frac{dJ}{dt} = \theta I + \sigma Q - (\gamma + \delta) J \\ \frac{dR}{dt} = \gamma J \end{cases} \tag{27}$$

方程中的参数满足 $0<k<1, 0<\epsilon + \lambda<1, 0<\theta+\delta<1, 0<\sigma<1, 0<\gamma+\delta<1$，可以利用公布的资料和实验方法加以确定。

设潜伏期为6天，其中后3天才有强传染性，于是 $\epsilon + \lambda = 1/3$，设潜伏期的已感染者（E）转入未隔离（I）和已隔离（Q）的比例为 $2:3$，可得 $\epsilon = 1/3 × 2/5 = 2/15, \lambda = 1/3 × 3/5 = 1/5$；设 I 和 Q 均约3天后转入治疗（J），于是 $\theta = \sigma = 1/3$；设治疗者（J）平均3周治愈，于是 $\gamma = 1/21$；死亡率取为 $\delta = 1/21 × 15/100 = 1/140$；取 k =0.1。

感染率 $\beta(t)$ 是模型中最重要的参数，从实际数据可知，在严格控制措施下 $\beta$ 是 $t$ 的减函数。经过多次数值计算确定 $\beta(t) = \frac{31+t}{22+5t}$。

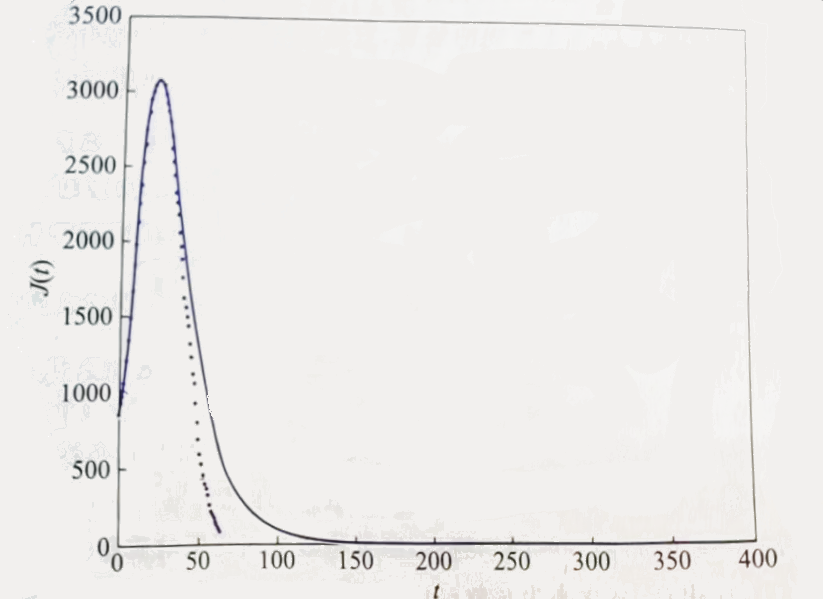
根据公布的数据，以2003年4月21日各个人群的数据为初始值：$E(0)=477, I(0)=286, Q(0)=191, J(0)=848, R(0)=1213$，将上面确定的参数代入模型（27），结果下图所示，实际数据与计算值相当接近（原文还有 $\theta$ 和 $k$ 取其他数值的计算结果，与实际数据相差较大）。

五、结果分析

以上3个模型以及许多参数论文都在SIR模型的基础上建立各具特色的微分方程（或差分形式）模型，差别主要是人群的划分和参数的定义。模型求解的结果是否与实际数据相吻合，关键之一在于参数估计。而一些参数能否得到比较恰当的估计，又依赖于是否有充分的数据。人群的细分必然要引进更多的参数，如果因为受限于能够得到的实际数据，致使某些参数无法或很难估计，那么即使模型很精细，也得不到好的结果。

【拓展练习】 SARS的传播

针对本教案给出的参数时变SIR模型进行改进，并利用改进后的模型对SARS的传播进行模拟，确保结果比本例的效果更好。可以考虑改变感染率 $\lambda(t)$ 和移除率 $\mu(t)$ 的拟合函数、取不同时期的数据进行拟合、将治愈者和死亡者人群进行分开考虑等。