【案例05】投资的收益和风险 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Python3.11
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用，请勿用作商用。

最后更新：2024年2月25日

【知识点】

数学规划、线性规划、整数规划

【问题描述】

例4.12（本题选自1998年全国大学生数学建模竞赛A题）
市场上有 nn 种资产（如股票、债券、……） si(i=1,2,...,n)s_i (i=1,2,...,n) 供投资者选择，某公司有数额为 MM 的一笔相当大的资金可用作一个时期的投资。公司财务分析人员对这 nn 种资产进行了评估，估算出在这一时期内购买资产 sis_i 的平均收益率为 rir_i，并预测出购买 sis_i 的风险损失率为 qiq_i。考虑到投资越分散，总的风险越小，公司确定，当用这笔资金购买若干种资产时，总体风险可用所投资的 sis_i 中最大的一个风险来度量。

购买 sis_i 要付交易费，费率为 pip_i，并且当购买额不超过给定值 uiu_i 时，交易费按购买 uiu_i 计算（不买当然无须付费）。另外，假定同期银行存款利率是 r0(r0=5%)r_0 (r_0 = 5\%) ，且既无交易费又无风险。

1). 试给该公司设计一种投资组合方案，即用给定的资金 MM，有选择地购买若干种资产或存银行生息，使净收益尽可能大，而总体风险尽可能小。已知 n=4n=4 时的相关数据如表1所示。

表1 四种资产的相关数据

资产 平均收益率 风险损失率 交易费率 定值费
sis_i rir_i (%) qiq_i (%) pip_i (%) uiu_i (元)
s1s_1 28 2.5 1 103
s2s_2 21 1.5 2 198
s3s_3 23 5.5 4.5 52
s4s_4 25 2.6 6.5 40

2). 试就一般情况对以上问题进行讨论，并利用 数据文件ex0412 中的数据进行计算。

【答案与解析】

一、问题分析

明确问题 这是一个组合投资问题：已知市场上可供投资的 n+1n+1 种资产的平均收益率、风险损失率以及购买资产时产生的交易费费率，设计一种投资组合方案，也就是要将可供投资的资金分成 n+1n+1 份分别购买 n+1n+1 种资产。不同类型的资产的平均收益率和风险损失率也各不相同，因此在进行投资时，要同时兼顾两个目标：投资的 净收益 和 风险。

二、模型假设

（1）可供投资的资金数额 MM 相当大；
（2）投资越分散，总的风险越小，总体风险可用所投资的 sis_i 中最大的一个风险来度量；
（3）可供选择的 n+1n+1 种资产（含银行存款）之间是相互独立的；
（4）每种资产可购买的数量为任意值；
（5）在当前投资周期内，ri,qi,pi,ui(i=0,1,...,n)r_i, q_i, p_i, u_i (i=0,1,...,n) 固定不变；
（6）不考虑在资产交易过程中产生的其他费用，如股票交易印花税等。

三、模型建立

设购买资产 sis_i 的金额为 xi(i=1,2,...,n)x_i (i=1,2,...,n)，存银行的金额为 x0x_0，投资组合向量记为 x=(x0,x1,...,xn)x=(x_0, x_1,...,x_n)，向量x是本问题的决策变量。题目中明确指出要考虑两类目标，即投资的净收益和风险，分别记为 V(x)V(x) 和 Q(x)Q(x)。

（1）购买 si(i=1,2,...,n)s_i(i=1,2,...,n) 时，需要支付一定的交易费，其费率为 pip_i。当购买额不超过给定值 uiu_i 时，支付的交易费按照 uiu_i 计算（不购买时无需付费），即为 piuip_i u_i；当购买额超过给定值 uiu_i 时，支付的交易费以实际交易额为准，即为 pixip_i x_i。所以，所付交易费 ci(xi)c_i(x_i) 是一个分段函数，即：

ci(xi)={pixi,xi≥ui,piui,0<xi<ui,0,xi=0.(1)c_i(x_i)= \left\{ \begin{array}{ll} p_i x_i, & x_i \geq u_i, \\\\ p_i u_i, & 0 < x_i < u_i, \\\\ 0, & x_i=0. \end{array} \right. \tag{1}

此处， c0(x0)=0c_0(x_0) = 0 表示存银行的金额 x0x_0。

（2）题目给出购买 sis_i 的平均收益率为 rir_i，因此投资 sis_i 的平均净收益为：

Vi(xi)=rixi−ci(xi),i=0,1,...,n(2)V_i(x_i) = r_i x_i - c_i(x_i), i=0,1,...,n \tag{2}

于是投资组合 xx 的平均净收益为：

V(x)=∑i=0nVi(xi)(3)V(x) = \sum^n_{i=0} V_i(x_i) \tag{3}

（3）购买 sis_i 的风险费率为 qiq_i，因此总体风险可以用所投资的 sis_i 中最大的一个风险来衡量，即：
Q(x)=max⁡{qixi∣i=0,1,2,...,n}.(4)Q(x) = \max\{q_i x_i | i=0,1,2,...,n\}. \tag{4}

（4）投资所需的总资金为：

I(x)=∑i=0n(xi+ci(xi))(5)I(x) = \sum^n_{i=0} (x_i + c_i(x_i)) \tag{5}

（5）为了满足题目要求的 净收益尽可能大，总体风险尽可能小，本题可以归结为一个多目标规划模型。

min⁡(Q(x),−V(x))s.t.I(x)=M,x≥0(7)\begin{aligned} & \min (Q(x), -V(x)) \\ s.t. & I(x) = M, x \geq 0 \end{aligned} \tag{7}

{max⁡∑i=0n(rixi−ci(xi))min⁡{max⁡0≤i≤n{qixi}}(7.1)\left\{ \begin{array}{ll} \max \sum^n_{i=0} (r_i x_i - c_i(x_i)) \\\\ \min \{\max\limits_{0 \leq i \leq n} \{q_i x_i\}\} \end{array} \right. \tag{7.1}

{∑i=0n(xi+ci(xi))=M,xi≥0(7.2)\left\{ \begin{array}{ll} \sum^n_{i=0} (x_i + c_i(x_i)) = M, & \\\\ x_i \geq 0 \end{array} \right. \tag{7.2}

（6）投资者在权衡资产风险和预期收益两方面时，希望选择一个令自己满意的投资组合。此时可以使用权重 ww 来权衡两个方面，当对风险和收益分别赋予权重 w(0≤w≤1)w (0 \leq w \leq 1) 和 (1−w)(1-w) 时，ww 称为投资偏好系数。
min⁡wQ(x)−(1−w)V(x)(8)\min wQ(x) - (1-w) V(x) \tag{8}

四、模型简化

在题设中，给定了公司提供的资金 MM 是一个相当大的值。相对而言，题目所给的定值 uiu_i（单位：元）相对总投资 MM 就变得很少，与交易费率 pip_i 相乘后的交易手续费 piuip_i u_i 就更小，这样购买 sis_i 的净收益 Vi(xi)V_i(x_i) 可以简化为 (ri−pi)xi(r_i - p_i)x_i。此时，目标函数（7）可以简化为：

{max⁡∑i=0n(ri−pi)xi,min⁡{max⁡0≤i≤n{qixi}}(9)\left\{ \begin{array}{ll} \max \sum^n_{i=0} (r_i - p_i)x_i, \\\\ \min \{\max\limits_{0 \leq i \leq n} \{q_i x_i\}\} \end{array} \right. \tag{9}

s.t.∑i=0n(1+pi)xi=M,xi≥0s.t. \sum^n_{i=0} (1 + p_i)x_i = M, x_i \geq 0

为了便于求解，我们可以进一步将模型（8）简化为以下三种情况：

4.1 模型一 固定风险水平，优化收益。

在实际投资中，投资者承受风险的程度不一样，若给定风险一个界限 α\alpha，使最大的一个风险 qixiM≤α\frac{q_i x_i}{M} \leq \alpha，可找到相应的投资方案。这样把多目标规划变成单目标的线性规划。

max⁡∑i=0n(ri−pi)xi(10)\max \sum^n_{i=0} (r_i - p_i) x_i \tag{10}

s.t.{qixiM≤α,i=1,2,..,n,∑i=0n(1+pi)xi=M,x≥0,i=0,1,...,n.s.t. \left\{ \begin{array}{ll} \frac{q_i x_i}{M} \leq \alpha, & i=1,2,..,n, \\ \\ \sum^n_{i=0} (1 + p_i) x_i = M, & \\ \\ x \geq 0, & i=0,1,...,n. \end{array} \right.

4.2 模型二 固定盈利水平，极小化风险。

若投资者希望总盈利至少达到水平 kk 以上，在风险最小的情况下寻求相应的投资组合。此时，多目标规划也简化为单目标的线性规划。

min⁡{max⁡0≤i≤n{qixi},\min \{\max_{0 \leq i \leq n} \{q_i x_i\},

s.t.{∑i=0n(ri−pi)xi≥kM,∑i=0n(1+pi)xi=M,xi≥0,i=0,1,...,n.s.t. \left\{ \begin{array}{ll} \sum^n_{i=0}(r_i - p_i) x_i \geq kM, \\ \\ \sum^n_{i=0} (1 + p_i) x_i = M, \\ \\ x_i \geq 0, & i=0,1,...,n. \end{array} \right.

4.3 模型三 两个目标函数加权求和。

根据模型公式（8），投资者在权衡资产风险和预期收益两方面时，希望选择一个令自己满意的投资组合。因此对风险、收益分别赋予权重 w(0≤w≤1)w (0 \leq w \leq 1) 和 (1−w)(1-w)后，模型可以简化为：

min⁡w{max⁡1≤i≤n{qixi}−(1−w)∑i=0n(ri−pi)xi,\min w \{\max_{1 \leq i \leq n} \{q_i x_i\} - (1-w) \sum^n_{i=0} (r_i - p_i) x_i,

s.t.{∑i=0n(1+pi)xi=M,xi≥0,i=0,1,...,n.s.t. \left\{ \begin{array}{ll} \sum^n_{i=0} (1 + p_i) x_i = M, & \\\\ x_i \geq 0, i=0,1,...,n. \end{array} \right.

五、模型求解与结果分析

首先，我们将题目给定的相关数据（表1）转换为矩阵形式，可得以下变量：

5.1 模型一的求解与分析

(1) 求解

设 M=10000M = 10000元，最高风险率 α=5%\alpha=5\%，并代入相关参数后，模型一可表示为：max⁡f=(ri−pi)xi=[0.05,0.27,0.19,0.185,0.185]⋅[x0,x1,x2,x3,x4]T\max f = (r_i-p_i)x_i = [0.05, 0.27, 0.19, 0.185, 0.185] \cdot [x_0, x_1, x_2, x_3, x_4]^T，

s.t.{x0+1.01x1+1.02x2+1.045x3+1.065x4=M,0.025x1≤αM.0.015x2≤αM.0.055x3≤αM.0.026x4≤αM.xi≥0,i=0,1,2,3,4.s.t. \left\{ \begin{array}{ll} x_0 + 1.01 x_1 + 1.02x_2 + 1.045x_3 + 1.065x_4 = M, \\ 0.025x_1 \leq \alpha M. \\ 0.015x_2 \leq \alpha M. \\ 0.055x_3 \leq \alpha M. \\ 0.026x_4 \leq \alpha M. \\ x_i \geq 0, i=0,1,2,3,4. \end{array} \right.

由于 α\alpha 是任意给定的风险度，到底怎样设置是没有准则的，不同的投资者有不同的风险度。因此，我们从 α=0\alpha=0 开始，以步长为 Δα=0.001\Delta \alpha = 0.001 进行循环搜索，以确定最优方案。编制Python程序如下：

# ch0609_ex4_12_1
import cvxpy as cp              # 载入凸优化包
import matplotlib.pylab as plt  # 载入绘图程序包
plt.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体 

q = plt.array([0.025, 0.015, 0.055, 0.026])  
r = plt.array([0.05, 0.27, 0.19, 0.185, 0.185])
x = cp.Variable(5, pos=True)
aep = plt.array([1, 1.01, 1.02, 1.045, 1.065])
obj = cp.Maximize(r @ x)
a = 0; aa = []; Q = []; X = []; M = 10000;             # 设置初始风险率为0，增长上限为0.05
while a <= 0.05:
    con = [aep @ x == M, cp.multiply(q, x[1:])<=a*M]
    prob = cp.Problem(obj, con)
    prob.solve(solver=cp.GLPK_MI)
    aa.append(a);                                      # aa用于保存不同风险下的风险率向量
    Q.append(prob.value)                               # 将不同风险下的收益保存进变量Q中，以便可视化
    X.append(x.value)                                  # X为投资组合向量
    a = a + 0.001

plt.figure(figsize=(6,3))
plt.plot(aa, Q, 'r*'); 
plt.xlabel('风险率a')
plt.ylabel('收益Q', rotation=0); 
plt.show()

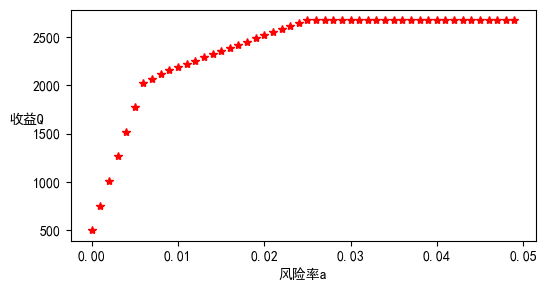
（2）结果分析

由以上风险 α\alpha 与收益 QQ 之间的关系可以得知

  1. 风险大，收益也大。
  2. 当投资越分散时，投资者承担的风险越小，这与题意一致。冒险的投资者会出现集中投资的情况，保守的投资者则尽量分散投资。
  3. 在 α=0.006\alpha=0.006 附近有一个转折点，在这一点左边，风险增加很少时，利润增长很快。在这一点右边，风险增加很大时，利润增长很缓慢，所以对于风险和收益没有特殊偏好的投资者来说，应该选择曲线的转折点作为最优投资组合，大约是 α=0.6%,Q=2000\alpha=0.6\%, Q=2000，所对应投资方案为风险度 α=0.006\alpha=0.006，收益 Q=2019.08Q=2019.08 元，x0=0x_0=0 元，x1=2400x_1=2400 元，x2=4000x_2=4000 元，x3=1090.91x_3=1090.91 元，x4=2212.21x_4=2212.21 元。
i = 6
print('当风险率为{}%时，\n 收益为：{:.2f}，\n 投资组合为：{}'.format(aa[i], Q[i], X[i]))

当风险率为0.006%时，
 收益为：2019.08，
 投资组合为：[0. 2400. 4000. 1090.90909091 2212.20657277]

5.2 模型三的求解与分析

（1）线性化

具体求解时，我们需要把目标函数线性化，引进变量 xn+1=max⁡1≤i≤n{qixi}x_{n+1} = \max\limits_{1 \leq i \leq n} \{q_i x_i\}，则模型可线性化为：

min⁡wxn+1−(1−w)∑i=0n(ri−pi)xi,\min w x_{n+1} - (1-w) \sum^n_{i=0} (r_i - p_i) x_i,

s.t.{qixi≤xn+1,i=1,2,...,n,∑i=0n(1+pi)xi=10000,xi≥0,i=0,1,...,n.s.t. \left\{ \begin{array}{ll} q_i x_i \leq x_{n+1}, i=1,2,...,n, \\\\ \sum^n_{i=0} (1 + p_i) x_i = 10000, \\\\ x_i \geq 0, i=0,1,...,n. \end{array} \right.

（2）求解及分析

当取不同的风险和收益预期权重 w∈[0,1]w \in [0, 1] 时，计算结果如 表2 所示，计算代码如下：

# ch0610_ex4_12_2
import numpy as np
import cvxpy as cp
import pylab as plt
import warnings
warnings.filterwarnings('ignore')
plt.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体 


plt.rc('font', family='SimHei')
plt.rc('font', size=15)
x = cp.Variable(6, pos = True)
r = np.array([0.05, 0.28, 0.21, 0.23, 0.25])
p = np.array([0, 0.01, 0.02, 0.045, 0.065])
q = np.array([0, 0.025, 0.015, 0.055, 0.026])


def LP(w):
    V = []  #风险初始化
    Q = []  #收益初始化
    X = []  #最优解的初始化
    W = []  # 权重系数初始化
    con = [(1+p) @ x[: -1] == 10000, cp.multiply(q[1:],x[1:5])<=x[5]]
    for i in range(len(w)):
        obj = cp.Minimize(w[i] * x[5] - (1-w[i]) *((r-p) @ x[: -1]))
        prob = cp.Problem(obj, con)
        prob.solve(solver='GLPK_MI')
        xx = x.value   #提出所有决策变量的取值
        V.append(max(q*xx[:-1]))
        Q.append((r-p)@xx[:-1])
        X.append(xx)
        W.append(w[i])
    print('w =', w); 
    print('V =', np.round(V,2))
    print('Q =', np.round(Q,2))
    plt.figure(figsize=(12,3)); 
    plt.grid('on')
    ax0 = plt.subplot(1,2,1)
    ax0.plot(V, Q, '*-'); 
    ax0.set_xlabel('风险（元）'); 
    ax0.set_ylabel('收益（元）')
    ax1 = plt.subplot(1,2,2)
    ax1.plot(w, Q, 'o-', color='red')
    ax1.set_ylabel('收益（元）')
    ax1.set_xlabel('权重系数w')
    ax2 = ax1.twinx()
    ax2.plot(w, V, '^-', color='blue')
    ax2.set_ylabel('风险（元）')

    return X

w1 = np.arange(0, 1.1, 0.1)
LP(w1); 
plt.show()

w = [0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]
V = [247.52 247.52 247.52 247.52 247.52 247.52 247.52 247.52  92.25  59.4
   0.  ]
Q = [2673.27 2673.27 2673.27 2673.27 2673.27 2673.27 2673.27 2673.27 2164.82
 2016.24  500.  ]

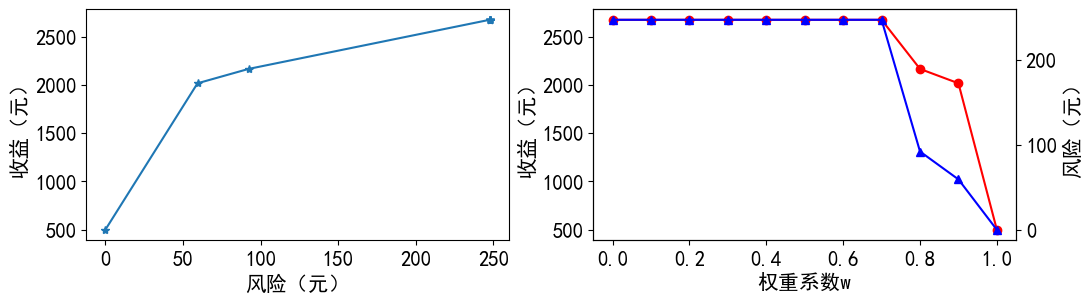
表2 风险与收益数据表（单位：元）

w 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
风险 247.52 247.52 247.52 247.52 247.52 247.52 247.52 247.52 92.25 59.4 0
收益 2673.27 2673.27 2673.27 2673.27 2673.27 2673.27 2673.27 2673.27 2164.82 2016.24 500

从以上数据可以看出，

为更好地描述收益和风险的对应关系，可将的取值进一步细化，只对0.7到1.0之间进行取值，对 ww 按照 0.01的间隔进行计算，此时可得表4.10（部分结果），绘制收益和风险的函数关系图像如图4.3所示。

表3 风险与收益数据表（单位：元）

w 0.766 0.767 0.810 0.811 0.824 0.825 0.962 0.963 1.0
风险 247.52 92.25 95.25 78.49 78.49 59.4 59.4 0 0
收益 2673.27 2164.82 2164.82 2105.99 2105.99 2016.24 2016.24 500 500

从 表3 可以看出，投资的收益越大，风险也越大。投资者可以根据自己对风险喜好的不同，选择合适的投资方案。曲线的拐点坐标约为 (59.4，2016.24)，此时对应的投资方案是购买资产 s1,s2,s3,s4,s5s_1, s_2, s_3, s_4, s_5 的资金分别为2375.84元、3959.73元、1079.93元、2284.46元和59.39元，存入银行的资金基本为0元（可以直接忽略），这对于风险和收益没有明显偏好的投资者是一个比较合适的选择。

w2 = np.array([0.7, 0.766, 0.767, 0.810, 0.811, 0.824, 0.825, 0.962, 0.963, 1.0])
X = LP(w2); 
print(X[-3]);  # 取拐点值0.962时的投资组合
plt.show()

w = [0.7   0.766 0.767 0.81  0.811 0.824 0.825 0.962 0.963 1.   ]
V = [247.52 247.52  92.25  92.25  78.49  78.49  59.4   59.4    0.     0.  ]
Q = [2673.27 2673.27 2164.82 2164.82 2105.99 2105.99 2016.24 2016.24  500.
  500.  ]
[4.54747351e-13 2.37583954e+03 3.95973257e+03 1.07992706e+03
 2.28446110e+03 5.93959885e+01]

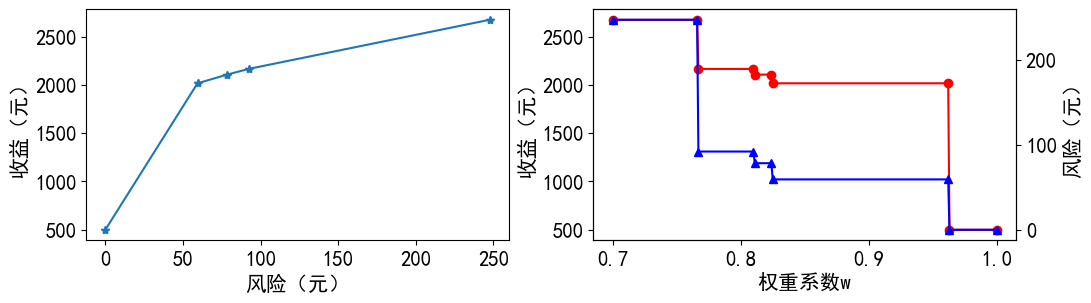
【拓展练习】 投资的收益和风险

（本题选自1998年全国大学生数学建模竞赛A题）

进一步完成原题中，第2小问的求解，要求在第1问的基础上给出完整的解题过程。

市场上有 nn 种资产（如股票、债券、……） si(i=1,2,...,n)s_i (i=1,2,...,n) 供投资者选择，某公司有数额为 MM 的一笔相当大的资金可用作一个时期的投资。公司财务分析人员对这 nn 种资产进行了评估，估算出在这一时期内购买资产 sis_i 的平均收益率为 rir_i，并预测出购买 sis_i 的风险损失率为 qiq_i。考虑到投资越分散，总的风险越小，公司确定，当用这笔资金购买若干种资产时，总体风险可用所投资的 sis_i 中最大的一个风险来度量。

购买 sis_i 要付交易费，费率为 pip_i，并且当购买额不超过给定值 uiu_i 时，交易费按购买 uiu_i 计算（不买当然无须付费）。另外，假定同期银行存款利率是 r0(r0=5%)r_0 (r_0 = 5\%) ，且既无交易费又无风险。

1). 试给该公司设计一种投资组合方案，即用给定的资金 MM，有选择地购买若干种资产或存银行生息，使净收益尽可能大，而总体风险尽可能小。已知 n=4n=4 时的相关数据如表1所示。

表1 四种资产的相关数据

资产 平均收益率 风险损失率 交易费率 定值费
sis_i rir_i (%) qiq_i (%) pip_i (%) uiu_i (元)
s1s_1 28 2.5 1 103
s2s_2 21 1.5 2 198
s3s_3 23 5.5 4.5 52
s4s_4 25 2.6 6.5 40

2). 试就一般情况对以上问题进行讨论，并利用 数据文件ex0412 中的数据进行计算。

【案例05】投资的收益和风险 返回首页

【知识点】

【问题描述】

【答案与解析】

【拓展练习】 投资的收益和风险

≡