【案例06】飞行管理问题返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Python3.11
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用，请勿用作商用。

最后更新：2024年3月17日

【知识点】

多目标规划、最优控制问题

【问题描述】

在约 10000m 高空的某边长 160km 的正方形区域内，经常有若干架飞机做水平飞行。区域内每架飞机的位置和速度向量均由计算机记录其数据，以便进行飞行管理。当一架欲进入该区域的飞机达到边缘时，记录其数据后，要立即计算并判断是否会与区域内的其他飞机发生碰撞。如果会碰撞，则应计算如何调整各架（包括新进入的）飞机飞行的方向角，以避免碰撞。先假设条件如下：
（1）不碰撞的标准为任意两架飞机的距离大于8km。
（2）飞机飞行方向角调整的幅度不应超过 $30^{\circ}$ 。
（3）所有飞机飞行速度均为 800km/h。
（4）进入该区域的飞机在到达区域边缘时，与区域内飞机的距离应在60km以上。
（5）最多需要考虑6架飞机。
（6）不必考虑飞机离开此区域后的状况。

试通过给定的假设条件，对这个避免碰撞的飞行管理问题建立数学模型，列出计算步骤，并对以下数据进行计算（方向角误差不超过 $0.01^{\circ}$ ），要求飞机飞行方向角调整的幅度尽量小。该区域4个顶点的坐标为 (0, 0), (160, 0), (160, 160), (0, 160)。记录数据如表1 所列。

表1 飞行记录数据

飞机编号	横坐标 $x$	纵坐标 $y$	方向角( $^{\circ}$ )
1	150	140	243
2	85	85	236
3	150	155	220.5
4	145	50	159
5	130	150	230
新进入	0	0	52

注：方向角指飞行方向与 $x$ 轴正方向的夹角。

【答案及解析】

一、问题分析

1.1 初步分析

在拿到问题（特别是不熟悉的问题）时，首先应该认真扣题，也就是抓住题目中的关键词“管理”进行联想。在考虑“管理”问题时，可以考虑先抓住一些字面容易理解的词汇：“碰撞”、“调整”、“避免碰撞”、“判断”等词进行联想；然后，再根据关键词“管理”进行进一步的联想，比如“管理”可以引申为“规划”、“调度”、“控制”等，再者，根据“管理”引申出的关键词，可以进一步联想出“多目标”、“多变量”、“多约束”、“多方案”等。
在进行初步联想的时候，一定要学会天马行空，不加约束地联想，最后将一些关键词进行组合，构建10-20个问题或者假设，为后一步选取主线、假设、限定以及问题拓展做基础。

为了便于理解题目的目的，我们可以考虑根据题目中的已知数据构建一些框架图或示意图，在本题中最直接的是构建6架飞机的初始状态图。下面给出使用Python绘制初始状态的代码。

import matplotlib.pyplot as plt  
import numpy as np  

# 1. 定义数据  
data = {  
    '编号': [1, 2, 3, 4, 5, 6],  
    '横坐标x': [150, 85, 150, 145, 130, 0],  
    '纵坐标y': [140, 85, 155, 50, 150, 0],  
    '方向角': [243, 236, 220.5, 159, 230, 52]  
}  
# 2. 转换为numpy数组  
x = np.array(data['横坐标x'])  
y = np.array(data['纵坐标y'])  
angles = np.radians(np.array(data['方向角']))  # 将角度转换为弧度  

# 2. 绘制基础坐标轴  
plt.figure(figsize=(5, 5))  
plt.gca().set_aspect('equal', adjustable='box')  # 保持x和y轴比例相同  
plt.xlim(0, 160)  # 设置x轴范围  
plt.ylim(0, 160)  # 设置y轴范围  

# 3. 绘制箭头  
for i in range(len(x)):  
    # 计算箭头长度和尾部的位置  
    arrow_length = 30  # 可以根据需要调整箭头的长度  
    dx = arrow_length * np.cos(angles[i])  
    dy = arrow_length * np.sin(angles[i])  
    tail_x = x[i] - dx / 2  
    tail_y = y[i] - dy / 2  
    head_x = x[i] + dx / 2  
    head_y = y[i] + dy / 2  

    # 绘制箭头  
    plt.arrow(tail_x, tail_y, dx, dy, head_width=3, head_length=4, fc='b', ec='b')  

# 4. 显示图形  
plt.grid(True)  # 添加网格  
plt.show()

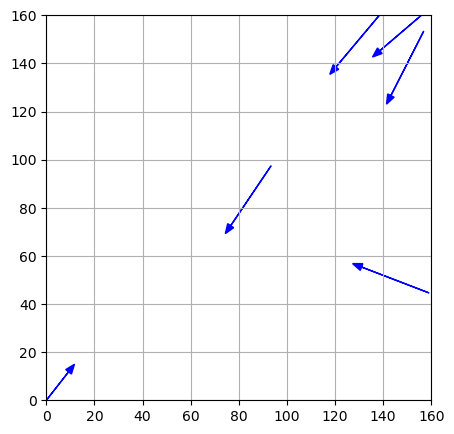
1.2 建模过程

由上图，我们可以看出本项目的问题从形式上看，应该属于最优控制问题，若需要同时考虑6架飞机，该问题便有6个可控制对象，这是比较复杂的问题。因此，

首先应考虑如何简化问题；
然后再从不同的侧重角度讨论并确定目标函数和约束条件，建立非线性模型；
接下来，根据计算的需要，将非线性模型进行线性化，并使用合适的方法进行求解；
在问题的最后，可以考虑利用逐步逼近搜索方法、能量梯度求解法、球状求解法等方法对该问题一开始引申出的假设和待定问题进行进一步的拓展讨论。

对于本项目，我们可以将以上内容总结为如下示意图：

1.3 重要假设分析

根据题意，要求飞机飞行方向角的调整要尽量小，我们可以得到以下两个重要假设：

如果飞机存在发生碰撞的可能，尽早调整一定优于晚调整

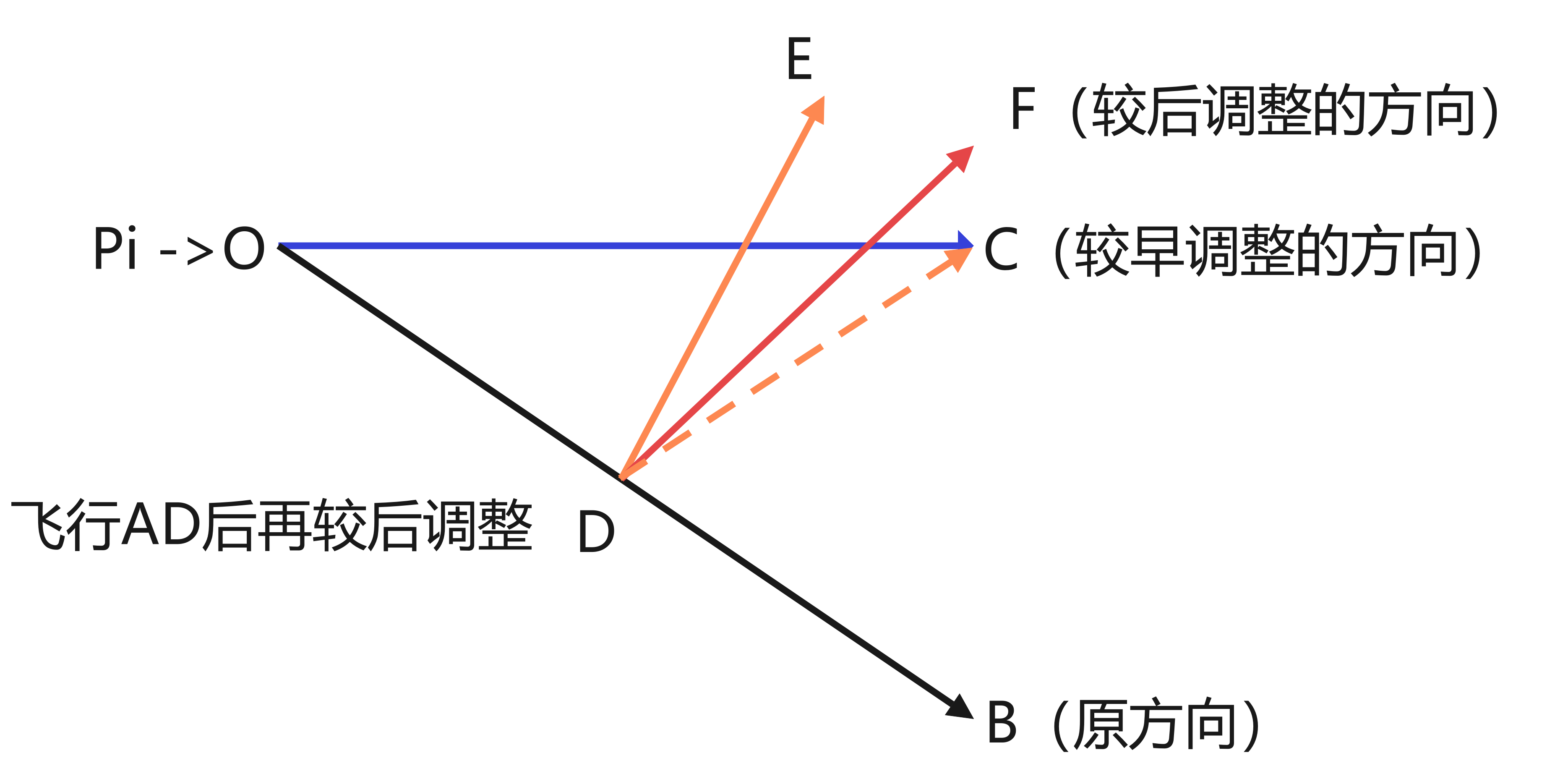
如上图所示，若OB是飞机 $P_i$ 的初始飞行方向，该方向有碰撞可能，OC为安全飞行路线。当飞机 $P_i$ 位于O点时，它只需要调整 $\angle BDC$ 即可到达安全航线。若在O点时，飞机错过了调整，而到达D点再进行调整，此时要飞向C点，则其调整角 $\angle BDC$ 显然大于原来的调整角 $\angle BOC$ 。此外，由于飞机在D点时具有初始速度，因此若要飞向C点，其实际的调整角应该大于 $\angle BDC$ ，而应该是 $\angle BOF$ 。考虑到飞机的持续飞行，甚至于要调整到DE的方向才能满足安全飞行，很显然，由于 $\angle BDE > \angle BDF > \angle BOC$ ，因此位于点D的调整角 $\angle BDE$ 更加糟糕！

如果飞机存在发生碰撞的可能，多次调整不如一次调整

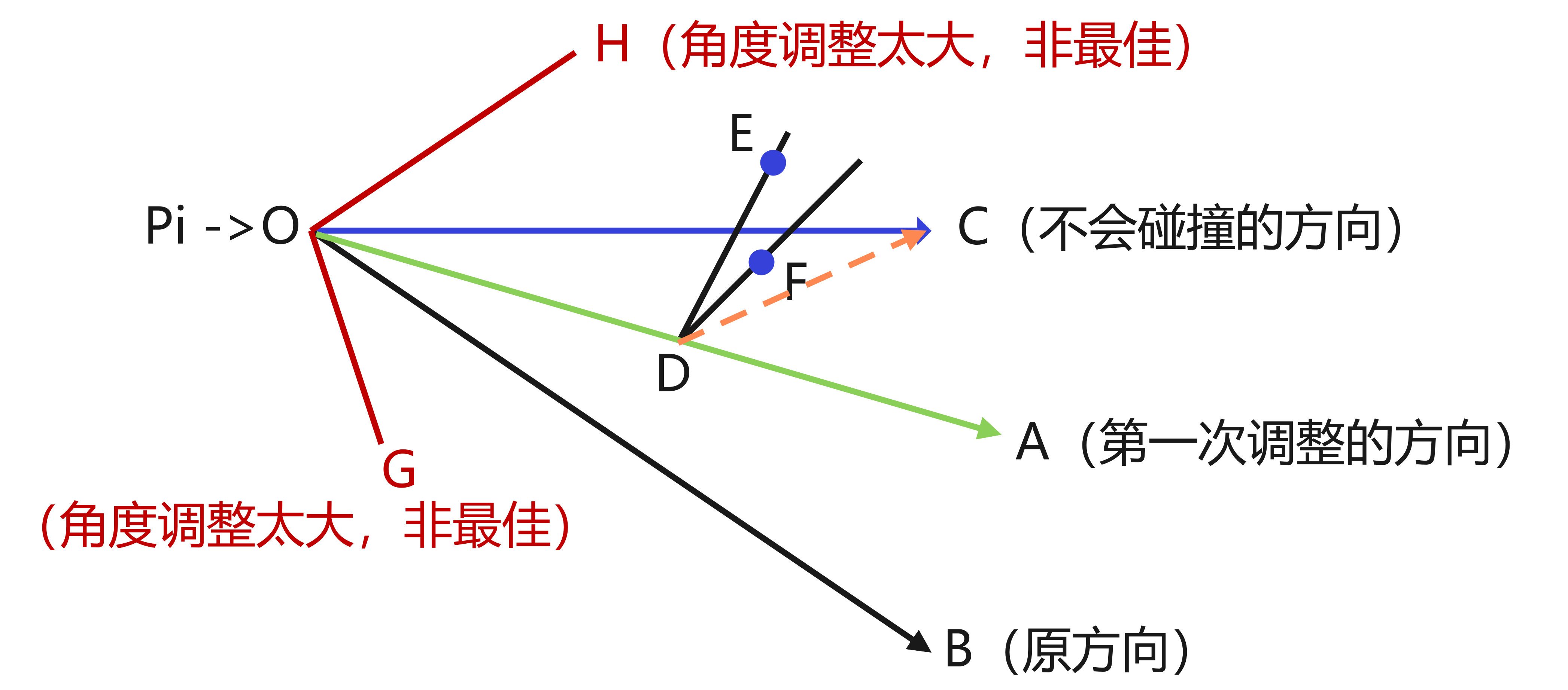
如上图所示，若飞机 $P_i$ 依然位于初始点O，且OB依然是初始飞行方向，OC是安全航线。假设需要经过多次调整才能到达安全航线，则 $\angle BOA, \angle BOH, \angle BOG$ 都是第一次可能调整的方向。这之中 $\angle BOH$ 显然过大，而 $\angle BOG$ 方向反了，都不是理想的调整位置。设第一次调整的位置为 $\angle BOA$ ，则当经过第二次或经过n次调整后，最终可以到达安全点C。与上一种假设类似，从D点要调整到C点，其实际调整角应该为 $\angle BOA + \angle ADE$ ，其结果远大于 $\angle BOA + \angle AOC = \angle BOC$ ，因此，多次调整也不如一次调整更好。

1.4 其他假设

飞机在锁定区域内作直线飞行，且永远不会偏离航线；
飞行管理系统不会发生意外，如发动机失灵，或其他导致飞机改变航向的意外；
飞机进入区域边缘时，立即做成计算，并根据计算结果立即进行方向角的调整（重要假设分析1）；
飞机管理系统发出指令后，应被飞机立即执行，即飞机的转向是瞬间完成的。忽略飞机转向时的转弯半径和转弯时间。
每架飞机在整个过程中只进行一次转向调整（重要假设分析2）。
新飞机进入监管区域时，以在监管区域内的飞机的飞行方向已经进行过调整，不会再发生碰撞。可能存在碰撞的只有新进入的飞机。

二、符号说明

$P_i$ 表示第 $i$ 架飞机，其中刚进入区域的飞机记作 $P_6$
$v_i(t)$ 表示第 $i$ 架飞机在 t 时刻的速度，在本题中速度为定值，可以用 $a$ 来表示这个飞机飞行速度的定值，记作 $a = 800km/h$
$(x^0_i, y^0_i)$ 为第 $i$ 架飞机的初始位置， $i=1,2,...,6, i=6$ 对应新进入的飞机
$(x_i(t), y_i(t))$ 为第 $i$ 架飞机在 $t$ 时刻的位置
$\theta^0_i$ 为第 $i$ 架飞机的初始方向角，即飞行方向与 $x$ 轴正向夹角， $0 \leq \theta^0_i \leq 2 \pi$
$\Delta \theta_i$ 为第 $i$ 架飞机的方向角调整量，逆时针方向为正，顺时针方向为负， $-\frac{\pi}{6} \leq \Delta \theta_i \leq \frac{\pi}{6}$
$\theta_i = \theta^0_i + \Delta \theta_i$ 为第 $i$ 架飞机调整后的飞行方向角

PS：不必强求一次写出所有符号的说明，可以考虑在完成模型的建立和求解后最后在进行整理。

三、模型建立

根据1.3节重要假设的分析，我们可以得到一个结论是新进入监控区域的飞机会根据当前区域内的飞机立即进行方向角的调整并且一次调整到位。基于这个结论，我们就可以根据表1 的数据来分析并确定飞机的初始状态和初始时飞机间的相互关系，从而求解避免碰撞的优化问题。

对于任何优化问题的求解，通常都需要确定两个重要数据：目标函数 和 约束条件。

3.1 目标函数

在本题中，目标函数为飞机 $P_6$ 到达安全航线的最小调整角，注意在调整过程中，由于新飞机 $P_6$ 的加入，原本处于控制区域内的其他飞机也存在调整的可能。因此，我们需要将飞机 $P_i, (i=1,2,...,6)$ 都纳入到优化的目标中。

设第 $i$ 架飞机的初始方向角为 $\theta^0_i$ ，经过调整（一次调整到位）后的方向为 $\theta_i = \theta^0_i + \Delta \theta_i$ 。根据题目要求的飞机飞行方向角调整幅度尽量小，可以得到目标函数：

$\min \sum_{i=1}^6 \mid \Delta \theta_i \mid \tag{1}$

注意：此处我们定义优化目标为所有飞机调整量的绝对值之和最小。但对于一个任务来说，可能会存在多种优化目标，这些优化目标有些是等价的，有些是不等价的，也有一些是不合理的。例如，针对本例的问题，还可以考虑使所有飞机的最大调整量最小、使所有飞机之间的相对距离最大、所有飞机以最少的距离飞离监控区域等。但应注意的是，如何正确地从中选取出最合适的目标函数。一般来说，目标函数的选择应紧扣题意，并且应注意目标函数应与约束条件相匹配，并且目标函数的选择应尽可能地使约束条件得到满足。

接下来，我们来讨论约束条件。

3.2 约束条件

3.2.1 约束条件建模分析

根据题目的要求，要确保所有飞机在飞离监控区域的过程中避免碰撞，则必须满足以下条件：
（1）任意两架飞机的距离大于 $8$ 公里。
（2）飞机飞行方向角的调整幅度不应超过 $30^{\circ}$ 。
（3）所有飞机飞行速度均为 800km/h。
（4）进入该区域的飞机在到达区域边缘时，与区域内飞机的距离应在60km以上。

以上约束条件均根据题意获得，但应注意的是对于有些问题，约束条件可能需要根据实际情况进行调整。例如，在某些情况下，可能需要对约束条件进行一定的放松，以使问题得到求解。

对于约束条件（1），假设任意两架飞机 $i$ 和 $j$ 之间的距离为 $d_{ij}$ ，则有：

$d_{ij} = \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2} > 8$

然而仔细思考，我们会发现位于监控区域中的飞机 $P_i$ 和 $P_j$ 在任意时刻的状态都是动态的，因此简单计算两者距离作为约束条件是不合理的。因此，约束条件（1）的实际情况应该是，对于任意时刻 $t$ ，都存在：

$d_{ij} (t)= \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2} > 8 \tag{2}$

以上约束条件是一个关于时间 $t$ 的函数，而时间 $t$ 是一个未知量（或隐变量），并不容易求得，为此，我们可以考虑先描述每架飞机的飞行轨迹，再根据飞行轨迹来判断飞机之间的相对距离。该过程，我们稍后再描述。

对于约束条件（2）可以直接根据前面定义的调整角变量列出方程，如下所示：

$\mid \Delta \theta_i \mid \leq 30 ^{\circ}, i,j=1,2,...,6 \tag{3}$

约束条件（3）是一个常数，可以在求解过程中直接代入。
约束条件（4）为初始条件。根据已经给出的数据，可以轻松验证其满足性，因此本模型的设计中可以不予考虑。

3.2.2 约束条件（1）的建模

接下来，我们将继续讨论约束条件（1）。根据相对运动的观点，在考查两架飞机 $P_i$ 和 $P_j$ 的相互关系时，不妨将飞机 $P_i$ 视为静止状态，而飞机 $P_j$ 以相对速度 $v$ 相对于飞机 $P_i$ 运动。

为了保证任意两架飞机的距离大于 $8$ 公里，如图1 所示，我们可以假设飞机 $P_i$ 附近存在一个半径为8km的禁飞区域。也就是说，除飞机 $P_i$ 以外，不允许任意其他飞机进入该区域。

图1 飞机 $P_i$ 和 $P_j$ 的相对关系图

假设在距离飞机 $P_i$ 一定距离的地方存在一架飞机 $P_j$ ，其初始飞行方向角为 $\beta^0_{ij}$ ，速度 $a=800km/h$ 。要确保 $P_j$ 和 $P_i$ 不发生碰撞，则经过时间 $t$ 后，飞机 $P_j$ 始终不会进入到飞机 $P_i$ 的禁飞区。若记 $\beta^0_{ij}$ 为调整前第 $j$ 架飞机相对于第 $i$ 架飞机的相对速度（矢量）与这架飞机连线（从 $j$ 指向 $i$ 的矢量）的夹角（以连线矢量为基准，逆时针方向为正，顺时针方向为负）。则 $\alpha ^0_{ij}$ 为飞机 $P_i$ 的禁飞方向角。设 $\Delta \beta_{ij}$ 为飞机 $P_j$ 的调整方向角，则调整后的方向角 $\beta^0_{ij} + \Delta \beta_{ij}$ 应满足如下约束：

$\begin{cases} \beta^0_{ij} + \Delta \beta_{ij} > \alpha ^0_{ij}, & \beta^0_{ij} > 0 \\ \beta^0_{ij} + \Delta \beta_{ij} < -\alpha ^0_{ij}, & \beta^0_{ij} < 0 \end{cases} \tag{4}$

以上约束也可表示为：

$\alpha ^0_{ij} < \beta^0_{ij} + \Delta \beta_{ij} < 2 \pi - \alpha ^0_{ij} \tag{5}$

为便于处理，我们将上述不碰撞条件整理为如下形式：

$\mid \beta^0_{ij} + \Delta \beta_{ij} \mid > \alpha^0_{ij} \tag{6}$

3.2.3 约束条件（1）关键超参数的计算

接下来，我们来探讨约束条件（1）中三个超参数 $\beta^0_{ij}, \Delta \beta_{ij}, \alpha^0_{ij}$ 的建模。

初始碰撞角 $\alpha^0_{ij}$

如图1 所示，两架飞机的初始相对距离 $d_{ij}(0)$ 为：

$d_{ij}(0) = \sqrt{(x^0_i - x^0_j)^2 + (y^0_i - y^0_j)^2} \tag{7}$

根据三角函数关系可以得到：

$\alpha^0_{ij} = \arcsin \frac{8}{d_{ij}(0)} \tag{8}$

飞机 $P_j$ 的初始方向角 $\beta^0_{ij}$

在图1 中， $\beta^0_{ij}$ 表示初始方向角，也即调整前第 $j$ 架飞机相对于第 $i$ 架飞机的相对速度（矢量）与这架飞机连线（从 $j$ 指向 $i$ 的矢量）的夹角（以连线矢量为基准，逆时针方向为正，顺时针方向为负）。该值由飞机进入监控区域时的速度方向决定，为便于分别计算 $x$ 方向和 $y$ 方向的速度，我们将该值转换为复数形式。

$\beta^0_{ij} =$ 相对速度 $v_{ij}$ 的幅角 - 从 $j$ 指向 $i$ 的连线矢量的幅角 $= \arg \frac{e^{\textbf{j} \theta^0_j} - e^{\textbf{j} \theta^0_i}}{(x_i + \textbf{j} y_i)-(x_j + \textbf{j} y_j)} (i,j=1,2,...,6)$ 。

注意，在上式中 $\textbf{j}$ 表示虚数单位。

飞机 $P_j$ 的调整方向角 $\Delta \beta_{ij}$

在图1 的直角坐标系中，我们可以使用两个速度 $v_j$ 和 $v_i$ 的差来表示它们的相对速度，其形式如：

$v = v_j - v_i = (a \cos \theta_j - a \cos \theta_i, a \sin \theta_j - a \sin \theta_i) \tag{9}$

在上式中， $\theta_i = \theta^0_i + \Delta \theta_i, \theta_j = \theta^0_j + \Delta \theta_j$ 分别表示飞机 $P_i, P_j$ 在调整后的方向。 $a \cos \theta_i$ 表示方向调整后飞机 $P_i$ 在 $x$ 方向上的飞行速度，类似地 $a \cos \theta_j$ 表示飞机 $P_j$ 在 $x$ 方向上的飞行速度，两者的差则为飞机 $P_i$ 与飞机 $P_j$ 在 $x$ 方向上的相对速度。同理， $a \sin \theta_i$ 表示飞机 $P_i$ 在 $y$ 方向上的飞行速度， $a \sin \theta_j$ 表示飞机 $P_j$ 在 $y$ 方向上的飞行速度，两者的差则为飞机 $P_i$ 与飞机 $P_j$ 在 $y$ 方向上的相对速度。

根据三角函数的计算规则，我们可以将公式（10）化简为：

$\begin{aligned} v & = 2a \sin \frac{\theta_j - \theta_i}{2} (-\sin \frac{\theta_j + \theta_i}{2}, \cos \frac{\theta_j + \theta_i}{2}) \\ & = 2a \sin \frac{\theta_j - \theta_i}{2} (\cos (\frac{\pi}{2} + \frac{\theta_j + \theta_i}{2}), \sin (\frac{\pi}{2} + \frac{\theta_j + \theta_i}{2})) \end{aligned} \tag{10}$

此时，若设 $\theta_j \geq \theta_i$ ，则飞机 $P_i$ 和 $P_j$ 的相对飞行方向角为 $\beta_{ij} = \frac{\pi}{2} + \frac{\theta_i + \theta_j}{2}$ 。于是，只要当相对飞行方向角 $\beta_{ij}$ 满足：

$\alpha ^0_{ij} < \beta_{ij} < 2 \pi - \alpha ^0_{ij} \tag{11}$

时，两飞机不可能相撞。联合（6）,（11）可得 $\mid \beta^0_{ij} + \frac{1}{2} (\Delta \theta_i + \Delta \theta_j) \mid > \alpha^0_{ij}$ 。

3.3 最终模型

根据以上分析，最终模型汇总如下：

$\begin{aligned} & \min \sum_{i=1}^6 \mid \Delta \theta_i \mid, \\ & s.t.\begin{cases} \mid \beta^0_{ij} + \frac{1}{2} (\Delta \theta_i + \Delta \theta_j) \mid > \alpha^0_{ij}, & i=1,2,...,5, j=i+1,2,...,6 \\ \mid \Delta \theta_i \mid \leq 30 ^{\circ}, & i,j=1,2,...,6 \\ \end{cases} \end{aligned} \tag{12}$

三、模型求解

利用Python程序，可求得 $\alpha^0_{ij}$ 的值如表2所列， $\beta^0_{ij}$ 的值如表3所列。

import numpy as np
import pandas as pd
from scipy.optimize import minimize

# 1. 定义初始变量及初始参数
x0 = np.array([150, 85, 150, 145, 130, 0])          # 设置初始横坐标
y0 = np.array([140, 85, 155, 50, 150, 0])           # 设置初始纵坐标
xy0 = np.vstack([x0, y0]).T                         # 组合飞机的初始坐标位置(x0, y0)
theta0 = np.array([243, 236, 220.5, 159, 230, 52])  # 设置初始方向角
d = np.zeros((6, 6))                                # 定义飞机间的初始相对距离矩阵
a0 = np.zeros((6, 6))                               # 定义飞机间的相对碰撞角
b0 = np.zeros((6, 6))                               # 定义飞机间的相对调整角

# 2. 计算目标函数及约束条件的相关超参数
# 2.1 根据初始位置计算飞机的初始距离矩阵
for i in range(6):
    for j in range(6):
        d[i ,j] = np.linalg.norm(xy0[i] - xy0[j])   # 根据公式（7）计算初始相对距离
d[d==0] = np.inf                                    # 自己到自己的距离设置成无穷远

# 2.2 根据初始距离计算初始碰撞角（公式8）
# 角度 = 弧度 × (180/π)
# 弧度 = 角度 × (π/180)
a0 = np.arcsin(8.0/d)*180/np.pi                     # 以角度表示

# 2.3 使用复数形式计算飞机的初始方向角
xy1 = x0 + 1j*y0                       # 将初始坐标位置转换为复数
xy2 = np.exp(1j*theta0*np.pi/180)      # 将初始方向转换为复数

for m in range(6):
    for n in range(6):
        if n!= m:
            b0[m,n] = np.angle((xy2[n] - xy2[m])/(xy1[m] - xy1[n]), deg=True)   # 计算初始方向角，angle()：返回复数的幅角主值，当deg=True时，返回角度

# 2.4 将初始碰撞角和初始调整角写入文件保存
with pd.ExcelWriter('../../Data/Project06/res_projct06.xlsx') as f:
    pd.DataFrame(a0).to_excel(f, 'a0')
    pd.DataFrame(b0).to_excel(f, 'b0')

# 3. 模型定义
# 3.1 目标函数
obj = lambda x:sum(np.abs(x))        # x 为\Delta \theta 序列，即6架飞机的调整角
    
# 3.2 约束条件
bd = [(-30,30) for i in range(6)]    # 约束条件2：飞机调整边界约束，即theta0的取值范围，此处使用优化的边界进行定义
theta0 = 30*np.random.rand(6)        # 使用随机初始化对调整变量进行初始化

cons = []                            # 初始化约束不等式，即约束条件1
for i in range(5):
    for j in range(i+1,6):
        cons.append({'type':'ineq','fun':lambda x: np.abs(b0[i,j] + (x[i] + x[j])/2) - a0[i,j]})  # 约束类型为不等式ineq

# 3.3 模型求解
res = minimize(obj, theta0, constraints=cons, bounds=bd)

# 4. 结果输出
print(res)
print('最优值：', np.round(res.fun, 4))
print('最优解：', np.round(res.x, 4))

 message: Optimization terminated successfully
 success: True
  status: 0
     fun: 0.7909290038642947
       x: [ 1.922e-06 -1.225e-07  6.312e-06 -4.362e-06  4.603e-01
            3.307e-01]
     nit: 34
     jac: [ 1.000e+00  1.000e+00  1.000e+00 -1.000e+00  1.000e+00
            1.000e+00]
    nfev: 275
    njev: 34
最优值： 0.7909
最优解： [ 0.     -0.      0.     -0.      0.4603  0.3307]

如上所示，最终可以获得的最优解为 $\Delta \theta_1 = \Delta \theta_2 = \Delta \theta_3 = \Delta \theta_4, \Delta \theta_5 = 0.612^{\circ}, \Delta \theta_6 = 0.5853^{\circ}$ 。需要注意的是，这里获得的每架飞机的调整量并不是定值，而是根据实际优化情况进行变化，但最优值，即总调整角 $\sum_{i=1}^6 = 0.7909^{\circ}$ 是不变的。

【案例06】飞行管理问题 返回首页