【案例07】慢跑者追逐问题 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Python3.11
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用，请勿用作商用。

最后更新：2024年3月28日

---

【知识点】

微分方程

【问题描述】

一个慢跑者在平面上按如下规律跑步

$$X = 10 + 20 \cos t, Y = 20 + 15 \sin t \tag{8.10.1}$$

突然有一只狗攻击他，这只狗从原点出发，以恒定速率 $w$ 跑向慢跑者，狗运动方向始终指向慢跑者。分别求出 $w=20, w=5$ 时，狗的运动轨迹。

【答案及解析】

一、问题分析及假设

根据题意，首先做如下定义：

1. 设时刻 $t$ 狗的坐标为 $(x(t), y(t))$，慢跑者坐标为 $(X(t), Y(t))$。
2. 慢跑者的初始坐标以时刻 $t=0$ 进行定义，狗的初始坐标为 $(0,0)$。
3. 狗的速度恒定为 $w$，并且始终指向慢跑者。
4. 要求给定狗的速度 $w_1 = 20, w_2 = 5$，分别给出狗的运动轨迹。

为了便于理解，我们首先绘制出狗和慢跑者的初始位置，同时给出慢跑者的运动曲线。

# Lec0408-1: 例8.10 初始状态
# 1. 绘制慢跑者随着t变化的运动轨迹
# 2. 绘制慢跑者、狗的初始位置、以及时刻t=1时慢跑者的位置
# 3. 绘制三个位置的距离连线

import matplotlib.pyplot as plt
import numpy as np

# 1. 定义慢跑者的位置方程  
def runner_position(t):  
    X = 10 + 20 * np.cos(t)  
    Y = 20 + 15 * np.sin(t)  
    return X, Y  

dt = 0.01               # 时间步长 
t_max = 2 * np.pi       # 时间周期，模拟慢跑者一圈的情况
t_vals = np.linspace(0, t_max, int(t_max / dt))                  # 定义周期时间点
runner_X, runner_Y = zip(*[runner_position(t) for t in t_vals])  # 生成慢跑者的轨迹坐标

# 2. 定义几个位置的坐标
x0, y0 = (0, 0)                                            # 狗的初始位置：原点
X0, Y0 = (runner_position(0)[0], runner_position(0)[1])    # 慢跑者的初始位置（t=0）
X1, Y1 = (runner_position(1)[0], runner_position(1)[1])    # 慢跑者t=1时的位置

# 3. 绘制慢跑者曲线方程以及慢跑者、狗的初始位置、以及时刻t=1时慢跑者的位置
plt.figure(figsize=(6, 4))
plt.plot(x0, y0, 'ro', label='Origin')
plt.plot(X0, Y0, 'bo', label='runner_start')
plt.plot(X1, Y1, 'k*', label='runner_stop')
plt.plot(runner_X, runner_Y, label='Runner') 
plt.legend(loc="lower right")
plt.grid(True)

# 4. 绘制三个位置的距离连线
plt.plot((x0, X1), (y0, Y1), 'g-')
plt.plot((x0, X0), (y0, Y0), 'g-')
plt.plot((X0, X1), (Y0, Y1), 'g-')
plt.show()

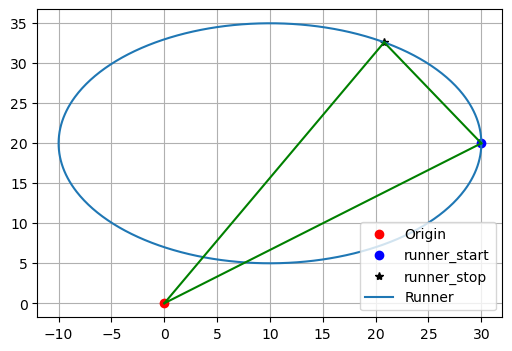
二、模型建立

接下来，我们给出狗的运动轨迹计算模型。根据三角形的毕达哥拉斯定理，可以得到狗的速度 $w$ 在 $x$ 和 $y$ 方向上的分量关系：

$$(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2 = w^2 \tag{8.10.2}$$

由于狗始终指向慢跑者，故狗的速度方向平行于狗与人位置的差向量，即：

$$\begin{bmatrix} \frac{dx}{dt} \\\\ \frac{dy}{dt} \end{bmatrix} = \lambda \begin{bmatrix} X-x \\\\ Y-y \end{bmatrix}, \lambda > 0 \tag{8.10.3}$$

将式（8.10.3）展开可得（8.10.4）得：
$$\begin{cases} \frac{dx}{dt} = \lambda (X - x) \\ \frac{dy}{dt} = \lambda (Y - y) \end{cases} \tag{8.10.4}$$

继续将（8.10.4）代入（8.10.2）并消去 $\lambda$ 后可以得到狗在 $t$ 时刻的坐标位置：
$$\begin{cases} \frac{dx}{dt} = \frac{w}{\sqrt{(X-x)^2 + (Y-y)^2}}(X - x) \\ \frac{dy}{dt} = \frac{w}{\sqrt{(X-x)^2 + (Y-y)^2}}(Y-y) \end{cases} \tag{8.10.5}$$

将人的位置方程（8.10.1）代入（8.10.5）可得狗的运动轨迹方程：
$$\begin{cases} \frac{dx}{dt} = \frac{w}{\sqrt{(10 + 20 \cos t - x)^2 + (20 + 15 \sin t-y)^2}}(10 + 20 \cos t - x) \\ \frac{dy}{dt} = \frac{w}{\sqrt{(10 + 20 \cos t - x)^2 + (20 + 15 \sin t-y)^2}}(20 + 15 \sin t-y) \\ x(0) = 0 \\ y(0) = 0 \end{cases} \tag{8.10.6}$$

三、编程求解

对于以上的运动轨迹方程，我们使用 odeint() 函数来求数值解。但为了进一步理解微元法，下面的代码我们通过定义狗和慢跑者关于时间 $t$ 的坐标位置函数 runner_position() 和 dog_position() 来衡量两者之间的距离。也就是说，当 $d=0$ 时，狗追上人。

在下面的代码中，我们通过定义一个数组变量 dist 来存储狗和慢跑者两者的距离，并判断 $dist$ 是否为0，若为0，则表示狗追上人。在实际代码编写中，由于慢跑者和狗的距离值较为敏感，因此，我们设置距离阈值 thres = 0.5，并以该阈值判断狗是否追上人。

下面给出速度 $w=20$ 时狗的运动轨迹曲线：

# Lec0408-2: 例8.10 慢跑者w=20
import numpy as np  
import matplotlib.pyplot as plt  

# 1. 定义慢跑者的位置方程  
def runner_position(t):  
    X = 10 + 20 * np.cos(t)  
    Y = 20 + 15 * np.sin(t)  
    return X, Y  

# 2. 狗的运动方程  
def dog_position(t, w, dt): 
    # 2.1 定义狗初始位置
    dog_X, dog_Y = 0, 0                           
    for _t in np.arange(0, t+dt, dt): 
        runner_X, runner_Y = runner_position(_t)  # 获取t时刻慢跑者的位置
        # 2.2 计算狗到慢跑者的向量  
        direction_X = runner_X - dog_X            # 公式8.10.3
        direction_Y = runner_Y - dog_Y  
        # 2.3 归一化向量以获取方向  
        direction_norm = np.sqrt(direction_X**2 + direction_Y**2) # 公式8.10.2
        if direction_norm > 0:  
            direction_X /= direction_norm         # 公式8.10.4
            direction_Y /= direction_norm  
        # 2.4 更新狗的位置  
        dog_X += w * dt * direction_X  
        dog_Y += w * dt * direction_Y
        dist = direction_norm
    return dog_X, dog_Y, dist, _t


# 绘制慢跑者和狗的运动轨迹  
def plot_trajectories(w, dt, t_max):  
    t_vals = np.linspace(0, t_max, int(t_max / dt))  # 时间点 
    thres = 0.1 
    stop_id = -1
    runner_X, runner_Y = zip(*[runner_position(t) for t in t_vals])  
    dog_X, dog_Y, dist, t = zip(*[dog_position(t, w, dt) for t in t_vals])
    try:
        stop_id = next(i for i, x in enumerate(dist) if x < thres)
    except:
        stop_id = -1
    t_meet = t_vals[stop_id]

    plt.figure(figsize=(12, 4))
    plt.subplot(121)  
    plt.plot(runner_X[:stop_id], runner_Y[:stop_id], label='Runner')    # 慢跑者轨迹
    plt.plot(dog_X[:stop_id], dog_Y[:stop_id], label='Dog')             # 狗的轨迹
    plt.plot(runner_X[0], runner_Y[0], 'bo', label='runner_start')      # 慢跑者的起点    
    plt.plot(0, 0, 'ro', label='Origin')                                # 狗的起点
    if stop_id != -1:                                                   # 当狗追不上时，不发生相遇
        plt.plot(dog_X[stop_id], dog_Y[stop_id], 'k*', label='meet_point')  # 相遇点
        plt.text(dog_X[stop_id]+1, dog_Y[stop_id], np.round(t_meet,4), fontsize=12, color='red')
    plt.axis('equal')  # 保持x轴和y轴的比例一致  
    plt.grid(True)  
    plt.legend()  
    plt.title(f'Trajectories of Runner and Dog (w={w}, dt={dt})')  
    plt.xlabel('X-coordinate')  
    plt.ylabel('Y-coordinate')  
    plt.subplot(122)
    plt.plot(t_vals, dist, label='Distance')
    plt.axhline(y=0, color='r', linestyle='--', label='Zero Distance')  # 标记距离为0的水平线  
    plt.grid(True)
    plt.legend()  
    plt.title(f'The distance between Runner and Dog (w={w})')  
    plt.xlabel('Time')  
    plt.ylabel('Distance') 
    plt.show()
    
# 设置狗的速度和模拟参数  
w = 20                  # 狗的速度  
dt = 0.01               # 时间步长  
t_max = 2 * np.pi       # 时间周期，模拟慢跑者一圈的情况 

# 绘制轨迹  
plot_trajectories(w, dt, t_max)

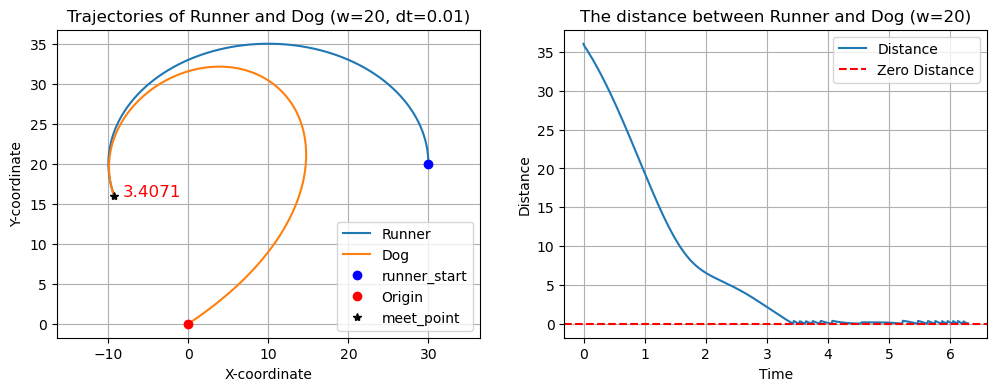
以下是速度 $w=5$ 时狗的运动轨迹曲线：

# Lec0408-3: 例8.10 慢跑者w=5

# 设置狗的速度和模拟参数  
w = 5                  # 狗的速度  
dt = 0.01               # 时间步长  
t_max = 5 * 2 * np.pi       # 时间周期，模拟慢跑者一圈的情况 

# 绘制轨迹  
plot_trajectories(w, dt, t_max)

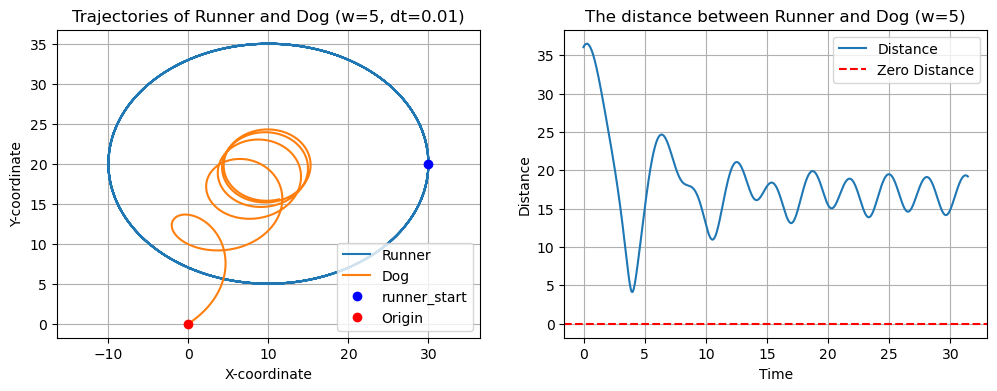
以下是速度 $w=10$ 时狗的运动轨迹曲线：

# Lec0408-4: 例8.10 慢跑者w=10

# 设置狗的速度和模拟参数  
w = 10                  # 狗的速度  
dt = 0.01               # 时间步长  
t_max = 5 * 2 * np.pi       # 时间周期，模拟慢跑者一圈的情况 

# 绘制轨迹  
plot_trajectories(w, dt, t_max)

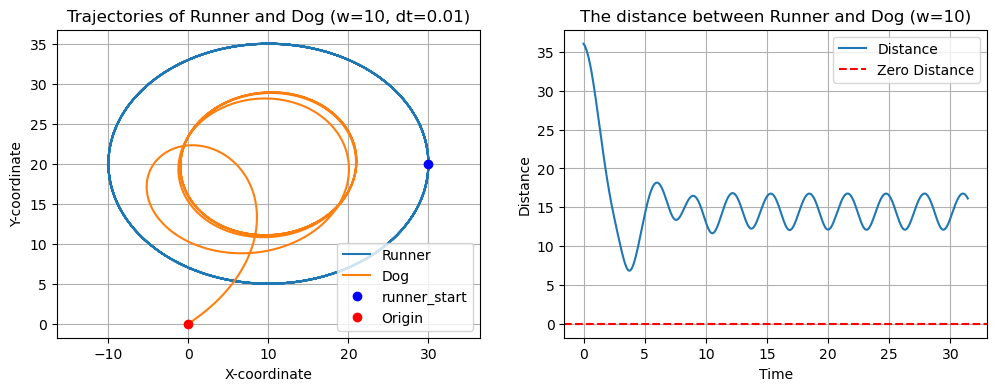
对上面的结果做一个总结，当狗的速度为 $w=20$ 时，狗在$t=3.4s$ 时，追上慢跑者，而当狗的速度为 $w=5$ 时，甚至是 $w=10$ 时，狗都始终无法追上慢跑者。

【拓展练习】

进一步推广，

1. 我们可以衡量狗的速度 $w$ 在什么范围内能够追上慢跑者；
2. 为了保证慢跑者不被狗追上，慢跑者应该如何调整他自己的速度等

请读者自行尝试。