【案例09】蠓虫分类判别 返回首页
作者:欧新宇(Xinyu OU)
当前版本:Release v1.0
开发平台:Python3.11
运行环境:Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用,请勿用作商用。
最后更新:2024年2月25日
【知识点】
分类、距离判别分析
【问题描述】
生物学家 Grogan 和 Wirth 曾就两种蠓虫 Af 和 Apf 的鉴别问题进行了研究,他们根据蠓虫的触角和翅长对蠓虫进行了分类,这种分类方法在生物学上是常用的。研究中他们对已经确定类别的6只Apf蠓虫和9只Af蠓虫的触角和翼长分别进行了测量,结果见 表1。
表1 蠓虫的触角和翼长的原始数据
| Af蠓虫 | 触角长 | 1.24 | 1.36 | 1.38 | 1.38 | 1.38 | 1.4 | 1.48 | 1.54 | 1.56 |
| 翼长 | 1.72 | 1.74 | 1.64 | 1.82 | 1.90 | 1.7 | 1.82 | 1.82 | 2.08 | |
| Apf蠓虫 | 触角长 | 1.14 | 1.18 | 1.20 | 1.26 | 1.28 | 1.30 | |||
| 翼长 | 1.78 | 1.96 | 1.86 | 2.00 | 2.00 | 1.96 | ||||
| 待判别样本x | 触角长 | 1.24 | 1.29 | 1.43 | ||||||
| 翼长 | 1.80 | 1.81 | 2.03 | |||||||
【提问】 我们的任务是利用这份数据来建立一种区分两种蠓虫的模型,用于对已知触角长和翅长的待判蠓虫样本进行识别,并着重讨论以下问题:
- 根据表1中给出的Apf蠓虫和Af蠓虫的触角和翅长数据,建立一个判别模型,用于对待判样本进行分类。
- 利用建立的判别模型,对表1中已知触角长和翼长的3个待判样本x进行分类,并给出分类结果。
- 如果Apf蠓虫是某种疾病的载体毒蠓,Af蠓虫是传粉益蠓,在这种情况下是否需要修改所用的分类方法,如何修改?
【答案与解析】
一、问题背景
本问题改编自1989年美国大学生数学建模竞赛的赛题,实际中经常会遇到这类数学建模问题,比如医生在掌握了以往各种疾病(如流感、肺炎、心肌炎等)的症状和体征后,利用统计学方法建立一个判别模型,用于对新的待诊断患者进行分类,从而确定其具体诊断结果,并判定其患病的类型;又如已知不同类型飞机的雷达反射波的各项特征指标,来判定一架飞机属于那种类型。这种在已知样本分类的前提下,利用已有的样本数据建立判别模型,用来对未知类别的新样本进行分类的问题属于统计学中的“判别分析”。目前,判别分析已经成为数据挖掘、机器学习、模式识别(语音识别、图像识别、指纹识别、文本识别)等领域的重要理论基础。
蠓虫分类判别属于判别分析,可以通过生物学家给出的9个Af蠓虫与6个Apf蠓虫作为训练样本,利用这些蠓虫的触角和翅长数据建立一个关于指标的判别函数和判别准则(判别模型),并由此对新的蠓虫样本进行分类,并且利用判别准则进行回判或交叉验证,以估计误判率。下面先利用距离判别方法建立比较简单的模型,再利用Bayes判别方法和SVM支持向量机方法处理需要区分毒蠓和益蠓的特殊情况。
二、问题分析
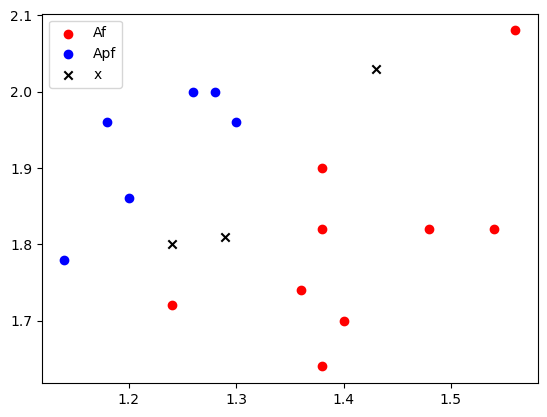
对 表1 蠓虫样本的数据做散点图,观察图形发现,Apf蠓虫的数据点集中在图的左上方,Af蠓虫的数据点集中在图的右下方,而3个带判样本处于两类点中间。这表明每类蠓虫的触角长和翼长两个指标之间相关的。直观的判别方法应该给是找一条线把这两类点分开,将它作为Apf蠓虫和Af蠓虫的分界线,依此构成判别准则,用于确定3个待判样本属于哪一类。
可视化原始数据的分布情况是对数据进行预处理和了解的一种常用方法,这种方法可以有效地快速掌握数据的分布特征,从而为后续的数据分析和建模提供依据。
以下给出本问题数据可视化的Python代码。
import matplotlib.pyplot as plt
f = open('../../Data/Project04/data_proj04.txt');
d = f.readlines()
a = [e.split() for e in d[0:2]] #提取Af字符串数据
a = np.array([list(map(eval, e)) for e in a])
b = [e.split() for e in d[2:4]] #提取Apf字符串数据
b = np.array([list(map(eval, e)) for e in b])
x = [e.split() for e in d[4:6]] #提取Apf字符串数据
x = np.array([list(map(eval, e)) for e in x])
plt.scatter(a[0], a[1], marker='o', color='r', label='Af')
plt.scatter(b[0], b[1], marker='o', color='b', label='Apf')
plt.scatter(x[0], x[1], marker='x', color='black', label='x')
plt.legend()
plt.show()
三、模型建立和求解
3.1 方法一:距离判别模型
3.1.1 模型假设和分析
假设Af蠓虫和Apf蠓虫的训练样本全部来自于样本空间 ,且 ,蠓虫样品的指标使用二维向量 表示,它们是平面上的一个点,其中 是触角长度, 为翼长。整个数据集共有15个样品,其中9个属于Af,6个属于Apf。
距离判别模型的基本思想是,恰当地定义每个类别的聚类中心以及每个样本与聚类中心的距离;然后计算待判定样本与两个聚类中心的距离,并以距离较近作为判别准则。
设存在所有样本的空间 的期望值均值向量 ,协方差矩阵为 。显然,均值向量 就是所有样本的聚类中心。此处,我们可以使用统计学中的马氏距离(Mahalanobis),样本 到总样本空间 的聚类中心的马氏距离定义为:
注意:在此处,马氏距离同时考虑了指标 (触角长)和 (翅长)之间的相关性及各自取值的分散性,而欧氏距离则把两个指标视为完全独立的变量,所以在制定判别标准时,马氏距离的计算结果往往比欧氏距离更合理。显然,当 为单位矩阵时,马氏距离与欧氏距离等价。
记两个样本空间 和 的期望值向量(聚类中心)分别为 和 ,协方差矩阵分别为 和 。对给定的样本 ,分别计算 到样本空间 和 的马氏距离的平方 和 。根据就近原则,若 ,则判定 ;否则判定 。由于
若记
则判别准则等价于:
称 为距离判别函数,它一般是 的二次函数,而当 时容易证明:
此时, 是 的一次函数,称为线性距离判别函数,并称 为判别系数。
3.1.2 模型选择
在实际应用中,每个类的期望向量(聚类中心) 及协方差矩阵 通常是未知的,因此需要用训练样本的数据来进行估计。设样本 取自类别空间 , 取自样本空间 ,分别计算样本的估计均值向量 :
和协方差矩阵 :
作为 及 的估计值。
当 时,我们使用估计的协方差矩阵 来代替(2)式中的 ,当 时,我们使用混合协方差矩阵 来代替式(5)中的 ,其形式定义为:
根据以上描述,在进行蠓虫分类判别时,首先要确定的是 Apf 蠓虫的样本空间 和 Af 蠓虫的类别空间 是否具有相同的协方差矩阵,这关系到我们在进行判别函数选择时,究竟使用线性判别函数还是二次判别函数。为此,需要先对两类别空间的协方差矩阵进行一致性检验(Box M检验),检验假设
由多元统计结果可以知道,对于二维类别空间,若 都服从正态分布,则该假设的统计量为:
其中 , 为类别数。
注意,此处在使用 Box M检验两个协方差矩阵一致性的时候,需要定义一个超参数 ,这个超参数称为检验水平,它被用来计算一个评价概率 ,若 ,则拒绝 假设,即认为 具有不同的协方差矩阵;否则接受 假设,即认为 具有相同的协方差矩阵。在本例的蠓虫分类问题中,若取 ,经编程计算,,故接受原假设 ,即可以使用线性判别函数来建立分类模型。
3.1.3 模型求解
根据 表1 的蠓虫样本数据,我们首先计算出样本空间 的均值和样本协方差阵,然后根据(8)式计算出混合协方差矩阵 。同时,我们使用 BoxM 一致性检验来协方差矩阵 的一致性。理论上,若一致性检验通过,则使用线性判别函数来建立分类模型;若一致性检验不通过,则使用二次判别函数来建立分类模型。
下面给出Python代码实现:
# codes04-01
# 计算样本的均值、协方差矩阵及两个空间协方差的一致性
import numpy as np
import scipy.stats as stats
# 1. 数据获取
f = open('../../Data/Project04/data_proj04.txt');
data = f.readlines()
Af = [e.split() for e in data[0:2]] # 提取Af样本数据
Af = np.array([list(map(eval, e)) for e in Af])
Apf = [e.split() for e in data[2:4]] # 提取Apf样本数据
Apf = np.array([list(map(eval, e)) for e in Apf])
x = [e.split() for e in data[4:6]] # 提取待测样本数据
x = np.array([list(map(eval, e)) for e in x])
n1 = Af.shape[1] # Af的数量
n2 = Apf.shape[1] # Apf的数量
# 2. 计算G1, G2的均值和协方差矩阵
mu1 = Af.mean(axis=1, keepdims=True);
s1 = np.cov(Af)
mu2 = Apf.mean(axis=1, keepdims=True);
s2 = np.cov(Apf)
# 3. 计算混合协方差矩阵
s = ((n1-1)*s1 + (n2-1)*s2)/(n1+n2-2)
# 4. 一致性判断
p = 2 # 类别数,即Af和Apf两类
df = p*(p+1)/2 # 自由度参数
c = (2*p**2+3*p-1)/(6*(p+1))*(1/(n1-1)+1/(n2-1)-1/(n1+n2-2))
M = (n1+n2-2)*np.log(np.linalg.det(s))-(n1-1)*np.log(np.linalg.det(s1))-(n2-1)*np.log(np.linalg.det(s2))
M0 = (1-c)*M
p0 = 1 - stats.chi2.cdf(M0, df)
print('评价概率 a = {:.4f}。'.format(p0))
print('mu1 = {}, mu2 = {}'.format(mu1, mu2))
print('Sigma1 = {} \n Sigma2 = {} \n Sigma = {}'.format(s1, s2, s))
评价概率 a = 0.4359。
mu1 = [[1.41333333]
[1.80444444]], mu2 = [[1.22666667]
[1.92666667]]
Sigma1 = [[0.0098 0.00808333]
[0.00808333 0.01687778]]
Sigma2 = [[0.00394667 0.00434667]
[0.00434667 0.00778667]]
Sigma = [[0.00754872 0.00664615]
[0.00664615 0.0133812 ]]
由以上评价概率的值判定,本模型可以使用线性判别函数。为便于进一步对比模型的性能,下面我们依然分别给出使用线性判别函数和二次判别函数建立的距离判别模型。
- 二次函数
根据以上代码得到样本空间 的样本均值和样本协方差阵分别为:
设任给一蠓虫 ,它到 Af 和 Apf 的马氏距离记作 ,则有:
这里求得
取判别函数:
判别准则为:
利用Python程序求得3个待判样本点的判别函数值分别为-0.5182, -2.0379, -1.5130,所以把3个待判样本点都判为属于Af。
对于已知的15个样本点,上述判别模型的误判率为0。
# codes04-02
# 使用二次函数构造模型,并对待测样本进行预测
import sympy as sp
from numpy.linalg import inv
sp.var('x1, x2');
X = sp.Matrix([x1, x2]) # X为列向量
d1 = (X-mu1).T@inv(s1)@(X-mu1); d1 = sp.expand(d1)
d2 = (X-mu2).T@inv(s2)@(X-mu2); d2 = sp.expand(d2)
W2 = d1 - d2
W2 = sp.lambdify('x1, x2', W2, 'numpy') # 将符号函数转换为numpy函数
for i in range(3):
pred = W2(x[0][i], x[1][i])[0][0]
if pred >= 0:
y = 'Af'
else:
y = 'Apf'
print('待测样本 {} 的预测概率为:{:.4f},类别为:{}'.format(x[:, i], pred, y))
print('\n 二次函数模型 W2(x) = ')
(d1 - d2)[0] # 输出二次模型W2(x)
待测样本 [1.24 1.8 ] 的预测概率为:-1.7611,类别为:Apf
待测样本 [1.29 1.81] 的预测概率为:-9.9230,类别为:Apf
待测样本 [1.43 2.03] 的预测概率为:-10.9033,类别为:Apf
二次函数模型 W2(x) =
- 线性判别函数
类似地,根据以上描述,我们可以使用 来表示最终的距离线性判别模型,其中 是模型的判别系数, 是模型的常数项, 是待测样。以下Python代码可以计算出模型对应的系数和常数项,即:
与此同时,根据判别模型,也可以得到待测样本的类别,分别为:Af, Apf, Apf。
# codes04-02
# 使用线性判别函数构造模型,并对待测样本进行预测
mu = 1/2 * (mu1 + mu2)
a = np.dot((mu2 - mu1).T, np.linalg.inv(s))
W1c = np.dot(-1/2 * (mu1 + mu2).T, a.T)
sp.var('x1, x2');
X = sp.Matrix([x1, x2]) # X为列向量
W1 = (X - mu).T@a.T
W1 = sp.lambdify('x1, x2', W1, 'numpy')
for i in range(3):
pred = W1(x[0][i], x[1][i])[0][0]
if pred >= 0:
y = 'Af'
else:
y = 'Apf'
print('待测样本 {} 的预测概率为:{},类别为:{}'.format(x[:, i], pred, y))
print('模型的判别系数为:{},常数项为{}。'.format(a, W1c))
待测样本 [1.24 1.8 ] 的预测概率为:2.1639577630378266,类别为:Af
待测样本 [1.29 1.81] 的预测概率为:-0.36727743121361023,类别为:Apf
待测样本 [1.43 2.03] 的预测概率为:-0.1474712878149962,类别为:Apf
模型的判别系数为:[[-58.23643793 38.05867025]],常数项为[[5.87153436]]。
3.1.4 模型校验
从以上的输出结果来看,我们发现两种模型在相同的输入下得到了不同的预测结果,这说明模型是有可能存在一定误差的。这种误差的存在会随着数据量的增加,任务难度的增加而逐渐的变大。因此,我们需要对模型进行进一步的检验,以确定模型的准确性,从而进一步提高设计模型的性能。对于线性模型(9)和二阶函数模型(10),通常由如下两种校验方法:
- 回代误判法
将取自样本空间 的 个训练样本和取自样本空间 的 个训练样本逐个会带到判别函数中,并判定其类别归属。若原本属于 的样本被判别为 的样本个数为 ;原本属于 的样本被判别为 的样本个数为 ,则回代误判率为:。
对于蠓虫分类判别问题,经Python编程计算,线性模型的回代误判率为:,二阶函数模型的回代误判率也为:。从结果来看,两个模型对于原始样本的误判率都为,说明两个模型的学习都还不错。但鉴于两个模型对三个预测样本的结果并不相同,因此可以估计的是其中一个模型有过拟合的问题。但我们缺乏预测样本的真实标签,因此无法判定究竟是哪个模型存在过拟合问题。
# 1. 线性模型:
pred_Af = W1(Af[0], Af[1])
pred_Apf = W1(Apf[0], Apf[1])
print('Af蠓虫样本的预测结果(负值为Af蠓虫)为: \n {}'.format(pred_Af))
print('Apf蠓虫样本的预测结果(正值为Apf蠓虫)为:\n {}'.format(pred_Apf))
n12 = np.sum(pred_Af > 0)
n21 = np.sum(pred_Apf < 0)
n1 = Af[0].shape[0]
n2 = Apf[0].shape[0]
p = (n12 + n21)/(n1 + n2)
print('线性模型的回代误判率为:{}'.format(p))
print('\n')
# 2. 二次模型:
pred_Af = W2(Af[0], Af[1])
pred_Apf = W2(Apf[0], Apf[1])
print('Af蠓虫样本的预测结果(负值为Af蠓虫)为: \n {}'.format(pred_Af))
print('Apf蠓虫样本的预测结果(正值为Apf蠓虫)为:\n {}'.format(pred_Apf))
n12 = np.sum(pred_Af > 0)
n21 = np.sum(pred_Apf < 0)
n1 = Af[0].shape[0]
n2 = Apf[0].shape[0]
p = (n12 + n21)/(n1 + n2)
print('二次模型的回代误判率为:{}'.format(p))
Af蠓虫样本的预测结果(负值为Af蠓虫)为:
[[[ -0.88073586 -7.107935 -12.07853079 -5.22797014 -2.18327652
-10.95973933 -11.05161394 -14.54580021 -5.81527471]]]
Apf蠓虫样本的预测结果(正值为Apf蠓虫)为:
[[[ 7.22642815 11.74753128 6.7769355 8.61096305 7.44623429
4.75915873]]]
线性模型的回代误判率为:0.0
Af蠓虫样本的预测结果(负值为Af蠓虫)为:
[[[-12.97889715 -41.25705218 -73.19180411 -30.97440883 -17.10856674
-64.87060285 -65.24629803 -90.50481922 -38.8551162 ]]]
Apf蠓虫样本的预测结果(正值为Apf蠓虫)为:
[[[ 8.80310918 14.47220702 9.24969427 11.82703423 10.16499472
5.27207084]]]
二次模型的回代误判率为:0.0
- 交叉验证法
从来自样本空间 的 个训练样本中,每次拿出一个做为验证样本,其余 个与来自样本空间 的 个一起,作为训练样本用于建立判别准则,用验证样本进行检验。然后换一个样本作为验证样本。在总共 次检验中误判的样本个数记为 。对来自样本空间 的 个训练样本完成同样的步骤,在总共 次检验中误判的样本个数为 ,则交叉验证误判率的估计值为 。
对于蠓虫分类判别问题,经Python编程计算,使用线性模型时,有一个Af蠓虫倍误判为Apf蠓虫。因此,,又 ,所以交叉验证误判率的估计值为 ;使用二阶函数模型时,,又 ,所以交叉验证误判率的估计值为 。
由此可以判定在蠓虫分类判别任务中,我们所设计的二次模型比线性模型要更好一些,这也进一步说明对于分类问题,较为复杂的模型通常能获得较好的拟合能力。
但应注意的是,当任务比较简单的时候,过于复杂的模型也可能会产生严重的过拟合问题,而导致性能下降。另一方面,在大数据环境中,较为复杂的模型也需要更多的计算时间和计算资源。
# codes04-02
# 使用交叉验证方法,分别对线性函数和二次函数进行验证,输出交叉验证误判率估计值。
import sympy as sp
from numpy.linalg import inv
# 1. 对线性函数进行交叉验证
# 1.1 对Af进行交叉验证
n12 = 0
n21 = 0
for i in range(n1):
Af_train = np.delete(Af, i, axis=1) # 从Af数据子集中取出一个元素作为验证样本,剩余元素作为训练数据
Af_test = Af[:, i] # 将取出的元素作为验证样本
Apf_train = Apf # Apf数据子集保持不变
mu1_CV = Af_train.mean(axis=1, keepdims=True) # 重新计算Af数据子集的均值
s1_CV = np.cov(Af_train) # 重新计算Af数据子集的方差
mu2_CV = Apf_train.mean(axis=1, keepdims=True);
s2_CV = np.cov(Apf_train)
n1_CV = Af_train.shape[1]
n2_CV = Apf_train.shape[1]
s_CV = ((n1_CV-1)*s1_CV + (n2_CV-1)*s2_CV)/(n1_CV+n2_CV-2) # 重新计算混合方差
mu_CV = 1/2 * (mu1_CV + mu2_CV) # 重新计算混合均值
a_CV = np.dot((mu2_CV - mu1_CV).T, np.linalg.inv(s_CV)) # 重新计算混合判别系数
W1c_CV = np.dot(-1/2 * (mu1_CV + mu2_CV).T, a_CV.T) # 重新计算参数Wc
sp.var('x1, x2');
X = sp.Matrix([x1, x2]) # X为列向量
W1_CV = (X - mu_CV).T@a_CV.T # 定义线性判别函数
W1_CV = sp.lambdify('x1, x2', W1_CV, 'numpy') # 将符号函数转换为numpy函数
pred = W1_CV(Af_test[0], Af_test[1]) # 使用验证数据子集进行预测
print('Af蠓虫样本的预测结果(负值为Af蠓虫)为: \n {}'.format(pred))
n12 = n12 + np.sum(pred > 0) # 统计预测错误的样本数
# 1.2 对Apf进行交叉验证
for i in range(n2):
Af_train = Af
Apf_train = np.delete(Apf, i, axis=1)
Apf_test = Apf[:, i]
mu1_CV = Af_train.mean(axis=1, keepdims=True)
s1_CV = np.cov(Af_train)
mu2_CV = Apf_train.mean(axis=1, keepdims=True);
s2_CV = np.cov(Apf_train)
n1_CV = Af_train.shape[1]
n2_CV = Apf_train.shape[1]
s_CV = ((n1_CV-1)*s1_CV + (n2_CV-1)*s2_CV)/(n1_CV+n2_CV-2)
mu_CV = 1/2 * (mu1_CV + mu2_CV)
a_CV = np.dot((mu2_CV - mu1_CV).T, np.linalg.inv(s_CV))
W1c_CV = np.dot(-1/2 * (mu1_CV + mu2_CV).T, a_CV.T)
sp.var('x1, x2');
X = sp.Matrix([x1, x2]) # X为列向量
W1_CV = (X - mu_CV).T@a_CV.T
W1_CV = sp.lambdify('x1, x2', W1_CV, 'numpy') # 将符号函数转换为numpy函数
pred = W1_CV(Apf_test[0], Apf_test[1])
# print('Apf蠓虫样本的预测结果(正值为Apf蠓虫)为:\n {}'.format(pred))
n21 = n21 + np.sum(pred < 0)
p = (n12 + n21)/(n1 + n2)
print('线性模型的回代误判率为:{:.4f}'.format(p))
# 2. 对二次函数进行交叉验证
# 2.1 对Af进行交叉验证
n12 = 0
n21 = 0
for i in range(n1):
Af_train = np.delete(Af, i, axis=1)
Af_test = Af[:, i]
Apf_train = Apf
mu1_CV = Af_train.mean(axis=1, keepdims=True)
s1_CV = np.cov(Af_train)
mu2_CV = Apf_train.mean(axis=1, keepdims=True);
s2_CV = np.cov(Apf_train)
n1_CV = Af_train.shape[1]
n2_CV = Apf_train.shape[1]
s_CV = ((n1_CV-1)*s1_CV + (n2_CV-1)*s2_CV)/(n1_CV+n2_CV-2)
sp.var('x1, x2');
X = sp.Matrix([x1, x2]) # X为列向量
d1_CV = (X-mu1_CV).T@inv(s1_CV)@(X-mu1_CV);
d1_CV = sp.expand(d1_CV)
d2_CV = (X-mu2_CV).T@inv(s2_CV)@(X-mu2_CV);
d2_CV = sp.expand(d2_CV)
W2_CV = d1_CV - d2_CV
W2_CV = sp.lambdify('x1, x2', W2_CV, 'numpy') # 将符号函数转换为numpy函数
pred = W2_CV(Af_test[0], Af_test[1])
# print('Af蠓虫样本的预测结果(负值为Af蠓虫)为: \n {}'.format(pred))
n12 = n12 + np.sum(pred_Af > 0)
# 2.2 对Apf进行交叉验证
for i in range(n2):
Af_train = Af
Apf_train = np.delete(Apf, i, axis=1)
Apf_test = Apf[:, i]
mu1_CV = Af_train.mean(axis=1, keepdims=True)
s1_CV = np.cov(Af_train)
mu2_CV = Apf_train.mean(axis=1, keepdims=True);
s2_CV = np.cov(Apf_train)
n1_CV = Af_train.shape[1]
n2_CV = Apf_train.shape[1]
s_CV = ((n1_CV-1)*s1_CV + (n2_CV-1)*s2_CV)/(n1_CV+n2_CV-2)
sp.var('x1, x2');
X = sp.Matrix([x1, x2]) # X为列向量
d1_CV = (X-mu1_CV).T@inv(s1_CV)@(X-mu1_CV);
d1_CV = sp.expand(d1_CV)
d2_CV = (X-mu2_CV).T@inv(s2_CV)@(X-mu2_CV);
d2_CV = sp.expand(d2_CV)
W2_CV = d1_CV - d2_CV
W2_CV = sp.lambdify('x1, x2', W2_CV, 'numpy') # 将符号函数转换为numpy函数
pred = W2_CV(Apf_test[0], Apf_test[1])
# print('Apf蠓虫样本的预测结果(正值为Apf蠓虫)为:\n {}'.format(pred))
n21 = n21 + np.sum(pred < 0)
p = (n12 + n21)/(n1 + n2)
print('二次模型的回代误判率为:{:.4f}'.format(p))
线性模型的回代误判率为:0.0667
二次模型的回代误判率为:0.0000
- 训练集+验证集+测试集
在大数据环境中,特别是面向深度学习的大数据环境中,最常用的是验证模型的方式是将数据集划分为 训练集+验证集+测试集 的结构来对模型进行训练和测试。
一般来说模型应当在训练集上进行训练,然后在测试集上进行评估。然而深度学习的模型训练是一个非常主观的过程。换句话说,在训练过程中存在大量的超参数需要选择,如何选择这些超参数并对这些超参数进行合理的组合是非常经验化的。更多的时候只能需要通过反复的实验来搜索和验证。因此我们需要一个与训练集和测试集完全不相交的数据集合来实现这些超参数的选择。这个数据集合就是验证集。
在深度学习的工程任务中,通常会将数据集划分为四个子集,分别是训练集、验证集、测试集和训练验证集,其中训练验证集是训练集和验证集的组合。下面,我们先来看看这四个数据子集是怎么进行划分的,并且它们之间有什么的关联和区别。
- 训练集(Training Set):用来对模型进行初步迭代训练的数据子集。
- 验证集(Validation Set):用于模型在初步迭代训练期间辅助训练过程的数据子集。它通过训练过程中的定期评估来实现超参数选择。
- 测试集(Test Set):在模型训练好之后,用来进行最终模型的性能评估。
- 训练验证集(Trainval Set):由训练集和验证集组合获得。用于在确定了超参数之后,对模型进行最终训练,并输出最终模型。
根据数据集的划分原则,我们可以得到这四个数据集的划分方法和使用时机。具体而言,这也是深度学习的基本训练过程,流程如下:
深度学习训练过程
- 将原始数据集按照一定的比例和规则划分为训练集(train)、验证集(val)和测试集(test),并将训练集和验证集进行组合,生成训练验证集(trainval)。
- 使用训练集和验证集对模型进行初步的迭代训练,其中训练集用于实现模型的迭代训练,验证集用于在训练过程中进行定期评估。迭代训练的次数可以根据验证集的结果反复执行多次,以获得最优的超参数设置。
- 使用第2步中所获得超参数,在训练验证集上进行迭代训练,训练结束时将获得最终模型(Final Model)。
- 使用测试集在最终模型上进行评估,并输出测试集上的评估结果。
对于深度学习中数据集的使用,还有几点需要特别注意。
(1)训练集和验证集都是模型初步训练时所使用的数据。其中训练集用于模型训练,验证集用于超参数的评估。在初步训练的迭代过程中,验证集不应该出现在模型的训练数据中,只能用来进行模型的验证。
(2)测试集在训练过程中是不可见的。在训练过程中能评估模型好坏的只能是验证集,而不应该在训练过程中直接使用测试集来评估模型。并且在任何时候都不能将测试集加入到训练集中参与模型的训练。测试集只能在最终模型训练好后,进行最终的性能评估时使用。
(3)为了更好地完成超参数选择,通常会将原始的训练集(即训练验证集)分割成新的训练集和验证集,然后在完成初步迭代训练的超参数选择之后,再将划分出来的新训练集和验证集合并在一起,当做训练数据进行统一训练。换句话说训练集和训练验证集都是拿来训练模型的,所不同的是前者用于初步训练并实现超参数的选择,而后者是在确定超参数之后用来完成最终模型的训练。一般来说,在相同的超参数设置下,在数据量更大的训练验证集上训练获得的性能要由于在划分出来的训练集上训练获得的性能。
(4)对于四个不同的数据子集,需要根据其功能和实际的应用场景选择不同的数据预处理和数据增广方法。
线性模型的回代误判率为:0.0667
二次模型的回代误判率为:0.0000
3.2 方法二:Bayes判别模型
3.3 方法三:SVM支持向量机模型
3.4 代码实现
下面我们调用 sklearn库来实现包括Bayes、SVM在内的网络模型,sklearn为我们提供了非常简洁的实现方法。最后,由于本例中的测试数据没有标签,因此我们依然调用sklearn来对训练集进行误判率和交叉验证误判率的评价。
1. 数据格式变换
首先,我们按照机器学习的习惯格式将数据转换成三个数据子集:
- 训练集数据(x_train):二维数组,第一个维度为样本维度,第二个维度为特征维度,其形态如:[[features, features, ...], [fearture, feature, ...].....]
- 训练集标签(y_train):一维数组,其形态如:[label, label, ...]
- 测试集数据(x_test):二维数组,形态与训练集类似,第一个维度为样本维度,第二个维度为特征维度,其形态如:[[features, features, ...], [fearture, feature, ...].....]
2. 模型定义、预测及评价
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier as KNN
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.model_selection import cross_val_score as cvs
from sklearn.naive_bayes import GaussianNB
model_knn = KNN(n_neighbors=2).fit(x_train, y_train)
pred_knn = model_knn.predict(x_test)
print('KNN模型分类结果:', ['Af' if i == 0 else 'Apf' for i in pred_knn])
print('KNN模型的回代误判率:', 1 - model_knn.score(x_train, y_train))
print('KNN模型的交叉验证误判率:', 1 - cvs(model_knn, x_train, y_train, cv=5))
model_mlp = MLPClassifier(hidden_layer_sizes=(10,5,10), solver='lbfgs', random_state=1, max_iter=1000).fit(x_train, y_train)
pred_mlp = model_mlp.predict(x_test)
print('MLP模型分类结果:', ['Af' if i == 0 else 'Apf' for i in pred_mlp])
print('MLP模型的回代误判率:', 1 - model_mlp.score(x_train, y_train))
print('MLP模型的交叉验证误判率:', 1 - cvs(model_mlp, x_train, y_train, cv=5))
Sigma = s # 调用混合协方差矩阵
model_dist = KNN(metric='mahalanobis', metric_params=dict(V=s)).fit(x_train, y_train)
pred_dist = model_dist.predict(x_test)
print('Mahalanobis模型分类结果:', ['Af' if i == 0 else 'Apf' for i in pred_dist])
print('Mahalanobis模型的回代误判率:', 1 - model_dist.score(x_train, y_train))
print('Mahalanobis模型的交叉验证误判率:', 1 - cvs(model_dist, x_train, y_train, cv=5))
model_lda = LDA().fit(x_train, y_train)
pred_lda = model_lda.predict(x_test)
print('LDA模型分类结果:', ['Af' if i == 0 else 'Apf' for i in pred_lda])
print('LDA模型的回代误判率:', 1 - model_lda.score(x_train, y_train))
print('LDA模型的交叉验证误判率:', 1 - cvs(model_lda, x_train, y_train, cv=5))
model_gnb = GaussianNB().fit(x_train, y_train)
pred_gnb = model_gnb.predict(x_test)
print('GaussianNB模型分类结果:', ['Af' if i == 0 else 'Apf' for i in pred_gnb])
print('GaussianNB模型的回代误判率:', 1 - model_gnb.score(x_train, y_train))
print('GaussianNB模型的交叉验证误判率:', 1 - cvs(model_gnb, x_train, y_train, cv=5))
KNN模型分类结果: ['Af', 'Apf', 'Apf']
KNN模型的回代误判率: 0.06666666666666665
KNN模型的交叉验证误判率: [0.33333333 0. 0.33333333 0. 0. ]
MLP模型分类结果: ['Af', 'Apf', 'Apf']
MLP模型的回代误判率: 0.0
MLP模型的交叉验证误判率: [0. 0. 0. 0. 0.]
Mahalanobis模型分类结果: ['Af', 'Apf', 'Apf']
Mahalanobis模型的回代误判率: 0.0
Mahalanobis模型的交叉验证误判率: [0. 0. 0. 0. 0.]
LDA模型分类结果: ['Af', 'Apf', 'Apf']
LDA模型的回代误判率: 0.0
LDA模型的交叉验证误判率: [0.33333333 0. 0. 0. 0. ]
GaussianNB模型分类结果: ['Af', 'Apf', 'Apf']
GaussianNB模型的回代误判率: 0.0
GaussianNB模型的交叉验证误判率: [0. 0. 0. 0. 0.]
【拓展练习】 乳腺肿瘤预测问题
已知8个乳腺肿瘤病灶组织的样本表11.3,其中前3个位良性肿瘤,后5个为恶性肿瘤。数据为细胞核显微图像的5个量化特征:细胞直径、质地、周长、面积和光滑度。根据已知样本对未知的3个样本进行距离判别、Fisher判别和神经网络(MLP)判别,并计算每种模型的回代误判率与5折交叉验证误判率。(要求写出完整的建模过程和代码过程)
表 11.3 乳房肿瘤病灶组织样本信息表
| 序号 | 细胞核直径 | 质地 | 周长 | 面积 | 光滑度 | 类型 |
|---|---|---|---|---|---|---|
| 1 | 13.54 | 14.36 | 87.46 | 566.3 | 0.09779 | 良性 |
| 2 | 13.08 | 15.71 | 85.63 | 520 | 0.1075 | 良性 |
| 3 | 9.504 | 12.44 | 60.34 | 273.9 | 0.1024 | 良性 |
| 4 | 17.99 | 10.38 | 122.8 | 1001 | 0.1184 | 恶性 |
| 5 | 20.57 | 17.77 | 132.9 | 1326 | 0.08474 | 恶性 |
| 6 | 16.69 | 21.25 | 130 | 1206 | 0.1096 | 恶性 |
| 7 | 11.42 | 20.38 | 77.58 | 386.1 | 0.1425 | 恶性 |
| 8 | 20.29 | 14.34 | 135.1 | 1297 | 0.1003 | 恶性 |
| 9 | 16.6 | 28.08 | 108.3 | 858.1 | 0.08455 | 待定 |
| 10 | 20.6 | 29.33 | 140.1 | 1265 | 0.1178 | 待定 |
| 11 | 7.76 | 24.54 | 47.92 | 181 | 0.05263 | 待定 |