【第06讲】数学规划模型 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Python3.11
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案为非完整版教案，请结合课程PPT使用。

最后更新：2024年4月9日

一、线性规划模型

例4.2（续例4.1）求解在例4.1中建立的线性规划模型 

# Lec0601：例4.2
import cvxpy as cp
from numpy import array
c = array([70, 50, 60])  #定义目标向量
a = array([[2, 4, 3], [3, 1, 5], [7, 3, 5]])  #定义约束矩阵
b = array([150, 160, 200])  #定义约束条件的右边向量
x = cp.Variable(3, pos=True)  #定义3个决策变量
obj = cp.Maximize(c@x)    #构造目标函数
cons = [a@x <=b]     #构造约束条件
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')   #求解问题
print('最优解为：', x.value)
print('最优值为：', prob.value)

最优解为： [15.90909091 29.54545455  0.        ]
最优值为： 2590.909090909091

例4.3 项目投资问题

某部门在今后五年内考虑给下列项目投资，已知：
A项目，从第一年到第四年每年年初需要投资，并于次年末回收本利115％；
B项目，从第三年初需要投资，到第五年末能回收本利125％，但规定最大投资额不超过4万元；
C项目，第二年初需要投资，到第五年末能回收本利140％，但规定最大投资额不超过3万元；
D项目，五年内每年初可购买公债，于当年末归还，并加利息6％。
该部门现有资金10万元，问它应如何确定给这些项目每年的投资额，使到第五年末拥有的资金的本利总额为最大？

# Lec0602：例4.3
import cvxpy as cp
x = cp.Variable((5,4), pos=True)
obj = cp.Maximize(1.15*x[3,0]+1.40*x[1,2]+1.25*x[2,1]+1.06*x[4,3])
cons = [x[0,0]+x[0,3]==100000,
    x[1,0]+x[1,2]+x[1,3]==1.06*x[0,3],
    x[2,0]+x[2,1]+x[2,3]==1.15*x[0,0]+1.06*x[1,3],
    x[3,0]+x[3,3]==1.15*x[1,0]+1.06*x[2,3],
    x[4,3]==1.15*x[2,0]+1.06*x[3,3],
    x[2,1]<=40000, x[1,2]<=30000]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print("最优值为：", prob.value)
print("最优解为：\n", x.value)

最优值为： 143750.0
最优解为：
 [[34782.60869565     0.             0.         65217.39130435]
 [39130.43478261     0.         30000.             0.        ]
 [    0.         40000.             0.             0.        ]
 [45000.             0.             0.             0.        ]
 [    0.             0.             0.             0.        ]]

例4.4 捷运公司的仓库问题

捷运公司在下一年度的1~4月的4个月内拟租用仓库堆放物资。已知各月所需仓库面积列于表4.2。仓库租借费用随合同期而定，期限越长，折扣越大，具体数字见表4.2。租借仓库的合同每月初都可办理，每份合同具体规定租用面积和期限。因此该公司可根据需要，在任何一个月初办理租借合同。每次办理时签一份合同，也可签若干份租用面积和租借期限不同的合同，试确定该公司签订租借合同的最优决策，使所付租借费用最小。

表4.2 所需仓库面积和租借仓库费用数据（面积单位：100 m2m^2）

月份 1 2 3 4
所需仓库面积 15 10 20 12
合同租借期限 1个月 2个月 3个月 4个月
合同期内的租费 2800 4500 6000 7300 
# Lec0603: 例4.4
import cvxpy as cp
x = cp.Variable((4,4), pos=True)
obj = cp.Minimize(2800*sum(x[:,0])+4500*sum(x[:3,1])+
    6000*sum(x[:2,2])+7300*x[0,3])
cons = [sum(x[0,:])>=15,
    sum(x[0,1:])+sum(x[2,:3])>=10,
    sum(x[0,2:])+sum(x[1,1:3])+sum(x[2,:2])>=20,
    x[0,3]+x[1,2]+x[2,1]+[3,0]>=12]
prob = cp.Problem(obj,cons)
prob.solve(solver='GLPK_MI')
print("最优值为：", prob.value)
print("最优解为：\n", x.value)

最优值为： 118400.0
最优解为：
 [[ 3.  0.  0. 12.]
 [ 0.  0.  0.  0.]
 [ 8.  0.  0.  0.]
 [ 0.  0.  0.  0.]]

例4.5 产销地最小费用运输问题

使用Python软件计算6个产地8个销地的最小费用运输问题。单位商品运价如表4.3所示。

表4.3 单位商品运价表

单位运价/销地/产地 B1 B2 B3 B4 B5 B6 B7 B8 产量
A1 6 2 6 7 4 2 5 9 60
A2 4 9 5 3 8 5 8 2 55
A3 5 2 1 9 7 4 3 3 51
A4 7 6 7 3 9 2 7 1 43
A5 2 3 9 5 7 2 6 5 41
A6 5 5 2 2 8 1 4 3 52
销量 35 37 22 32 41 32 43 38   
#Lec0604: 例4.5-1
import numpy as np
import cvxpy as cp
import pandas as pd

# 1. 数据载入（txt）
c = np.genfromtxt("../Data/Lec06/data4_5_1.txt", dtype=float, max_rows=6, usecols=range(8)) #读前6行前8列数据
e = np.genfromtxt("../Data/Lec06/data4_5_1.txt", dtype=float, max_rows=6, usecols=8) #读最后一列数据
d = np.genfromtxt("../Data/Lec06/data4_5_1.txt", dtype=float, skip_header=6) #读最后一行数据

# 2. 
x = cp.Variable((6,8), pos=True)
obj =cp.Minimize(cp.sum(cp.multiply(c, x)))
con = [cp.sum(x, axis=0)==d, cp.sum(x, axis=1)<=e]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print("最优值为:", prob.value)
print("最优解为：\n", x.value)
xd=pd.DataFrame(x.value)
xd.to_excel("../Data/Lec06/output_4_5_1.xlsx")  #数据写到Excel文件，便于做表使用

最优值为: 664.0
最优解为：
 [[ 0. 19.  0.  0. 41.  0.  0.  0.]
 [ 0.  0.  0. 32.  0.  0.  0.  1.]
 [ 0. 12. 22.  0.  0.  0. 17.  0.]
 [ 0.  0.  0.  0.  0.  6.  0. 37.]
 [35.  6.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0. 26. 26.  0.]]

#Lec0604: 例4.5-2
import numpy as np
import cvxpy as cp
import pandas as pd

# 1. 数据载入（Excel）
data = pd.read_excel("../Data/Lec06/data4_5_2.xlsx", header=None)
data = data.values
c = data[:-1, :-1]
d = data[-1, :-1]
e = data[:-1, -1]

x = cp.Variable((6,8), pos=True)
obj =cp.Minimize(cp.sum(cp.multiply(c, x)))
con = [cp.sum(x, axis=0)==d, cp.sum(x, axis=1)<=e]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print("最优值为:", prob.value)
print("最优解为：\n", x.value)
xd = pd.DataFrame(x.value)
xd.to_excel("../Data/Lec06/output_4_5_2.xlsx")  #数据写到Excel文件，便于做表使用

最优值为: 664.0
最优解为：
 [[ 0. 19.  0.  0. 41.  0.  0.  0.]
 [ 0.  0.  0. 32.  0.  0.  0.  1.]
 [ 0. 12. 22.  0.  0.  0. 17.  0.]
 [ 0.  0.  0.  0.  0.  6.  0. 37.]
 [35.  6.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0. 26. 26.  0.]]

二、整数规划模型

例4.9 生产线问题

为了生产的需要，某工厂的一条生产线需要每天24小时不间断运转，但是每天不同时间段所需要的工人最低数量不同，具体数据如表4.5所示。已知每名工人的连续工作时间为8小时。则该工厂应该为该生产线配备多少名工人，才能保证生产线的正常运转？

# Lec0605：例4.9
import cvxpy as cp
x=cp.Variable(6, integer=True)
obj=cp.Minimize(sum(x))
cons=[x[0]+x[5]>=35, x[0]+x[1]>=40,
    x[1]+x[2]>=50, x[2]+x[3]>=45,
    x[3]+x[4]>=55, x[4]+x[5]>=30,
    x>=0]
prob=cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print("最优值为：", prob.value)
print("最优解为：", x.value)

最优值为： 140.0
最优解为： [35.  5. 45. 25. 30.  0.]

# Lec0605：例4.9-续（求余法）
import cvxpy as cp
import numpy as np

a=np.array([35,40,50,45,55,30])
x=cp.Variable(6, integer=True)
obj=cp.Minimize(sum(x)); cons=[x>=0]
for i in range(6):
    cons.append(x[(i-1)%6]+x[i]>=a[i])
prob=cp.Problem(obj,cons)
prob.solve(solver='GLPK_MI')
print("最优值为：",prob.value)
print("最优解为：",x.value)

最优值为： 140.0
最优解为： [35.  5. 45. 25. 30.  0.]

例4.10 超市装修任务分配

某连锁超市经营企业为了扩大规模，新租用五个门店，经过装修后再营业。现有四家装饰公司分别对这五个门店的装修费用进行报价，具体数据如表4.6所示。为保证装修质量，规定每个装修公司最多承担两个门店的装修任务。则为节省装修费用，该企业该如何分配装修任务？

# Lec0607: 例 4.10
import cvxpy as cp
import numpy as np
c = np.loadtxt('../Data/Lec06/data4_10.txt')
x = cp.Variable((4,5), integer=True)  #定义决策变量
obj = cp.Minimize(cp.sum(cp.multiply(c,x)))    #构造目标函数
cons = [0<=x, x<=1, cp.sum(x, axis=0)==1, cp.sum(x, axis=1)<=2]     #构造约束条件
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')   #求解问题
print('最优解为：\n', x.value)
print('最优值为：', prob.value)

最优解为：
 [[0. 0. 1. 0. 0.]
 [0. 0. 0. 1. 0.]
 [1. 1. 0. 0. 0.]
 [0. 0. 0. 0. 1.]]
最优值为： 63.8

例4.11 最小供应站的个数

已知10个商业网点的坐标如表4.7所示，现要在10个网点中选择适当位置设置供应站，要求供应站只能覆盖10公里之内的网点，且每个供应站最多供应5个网点，如何设置才能使供应站的数目最小，并求最小供应站的个数。

表4.7 商业网点的坐标和坐标数据
9.4888 8.7928 11.5960 11.5643 5.6756 9.8497 9.1756 13.1385 15.4663 15.5464
5.6817 10.3868 3.9294 4.4325 9.9658 17.6632 6.1517 11.8569 8.8721 15.5868 
# Lec0608_ex4_11
import cvxpy as cp
import numpy as np
a = np.loadtxt("../Data/Lec06/data4_11.txt")
d = np.zeros((10,10))
for i in range(10):
    for j in range(10):
        d[i,j] = np.linalg.norm(a[:,i]-a[:,j])
x = cp.Variable(10, integer=True)
y = cp.Variable((10, 10),integer=True)
obj = cp.Minimize(sum(x))
con = [sum(y)>=1, cp.sum(y,axis=1)<=5, x>=0, x<=1, y>=0, y<=1]

for i in range(10):
    con.append(x[i]==y[i,i])
    for j in range(10):
        con.append(d[i,j]*y[i,j]<=10*x[i])
        con.append(x[i]>=y[i,j])
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print("最优值为:", prob.value)
print("最优解为：\n", x.value)
print('----------\n', y.value)

最优值为: 2.0
最优解为：
 [0. 1. 0. 0. 0. 0. 0. 0. 1. 0.]
----------
 [[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [1. 1. 1. 0. 1. 1. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 1. 1. 1. 1.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]

三、投资的收益与风险

（本题选自1998年全国大学生数学建模竞赛A题）

本案例的详细教案请访问 Project05投资的收益和风险

四、非线性规划

例5.1 试分析并求解非线性规划

min⁡f(x)=x12+x22−4x1+4s.t.{g1(x)=−x1+x2−2≤0g2(x)=x12−x2+1≤0x1,x2≥0\min f(x) = x^2_1 + x^2_2 -4x_1 + 4 \\\\ s.t.\begin{cases} g_1(x) = - x_1 + x_2 - 2 \leq 0 \\ g_2(x) = x_1^2 - x_2 + 1 \leq 0 \\ x_1, x_2 \geq 0 \end{cases}

# Lec0609 例5.1
import numpy as np
import cvxpy as cp

x = cp.Variable(2,pos=True)
obj = cp.Minimize(sum(x**2)-4*x[0]+4)
con = [-x[0]+x[1]-2<=0, x[0]**2-x[1]+1<=0]
prob = cp.Problem(obj, con)
prob.solve(solver='CVXOPT')
print("最优值为:",round(prob.value,4))
print("最优解为:", np.round(x.value,4))

最优值为: 3.7989
最优解为: [0.5536 1.3064]

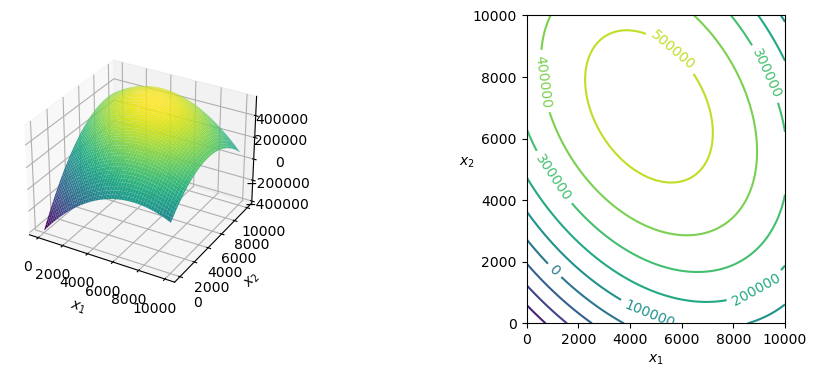
例5.2 彩色电视机生产计划

一家彩电制造商计划推出两种新产品：一种19英寸液晶平板电视机，制造商建议零售价为339美元；另一种21英寸液晶平板电视机，零售价为399美元。公司付出的成本为19英寸彩电每台195美元，21英寸彩电每台225美元，还要加上400000美元的固定成本。在竞争的销售市场中，每年售出的彩电数量会影响彩电的平均售价。据统计，对每种类型的彩电，每多售出一台，平均销售价格会下降1美分。而且19英寸彩电的销售会影响21英寸彩电的销售，反之亦然。据估计，每售出一台21英寸彩电，19英寸彩电的平均售价会下降0.3美分，而每售出一台19英寸彩电，21英寸彩电的平均售价会下降0.4美分。问题是：每种彩电应该各生产多少台？

# Lec0610 例5.2
import sympy as sp
import pylab as plt
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)

plt.rc('text', usetex=False)  #使用LaTeX字体
plt.rc('font', size=10)
sp.var('x1, x2')  #定义符号变量
y = (339-0.01*x1-0.003*x2)*x1+(399-0.004*x1-0.01*x2)*x2-(400000+195*x1+225*x2)
y = sp.simplify(y)   #化简
dy1 = y.diff(x1)     #求关于x1的偏导
dy2 = y.diff(x2)     #求关于x2的偏导
s = sp.solve([dy1, dy2], [x1, x2])
x10 = round(float(s[x1]))   #取整
x20 = round(float(s[x2]))
y0 = y.subs({x1: x10, x2: x20})  #符号函数代入数值

f = sp.lambdify('x1, x2', y, 'numpy')  #符号函数转换为匿名函数
x = plt.linspace(0, 10000, 100)
X, Y = plt.meshgrid(x, x)  #转换为网格数据
Z = f(X, Y)
plt.figure(figsize=(10, 4))
plt.subplots_adjust(wspace = 1)
ax = plt.subplot(121, projection='3d')  #第一个子窗口三维画图
ax.plot_surface(X, Y, Z,cmap='viridis')
ax.set_xlabel('$x_1$'); 
ax.set_ylabel('$x_2$')
plt.subplot(122)               # 激活第二个子窗口
contr = plt.contour(X,Y,Z,10)  # 10条等高线
plt.clabel(contr)              # 等高线标注
plt.ylabel('$x_2$', rotation=0)
plt.xlabel('$x_1$')

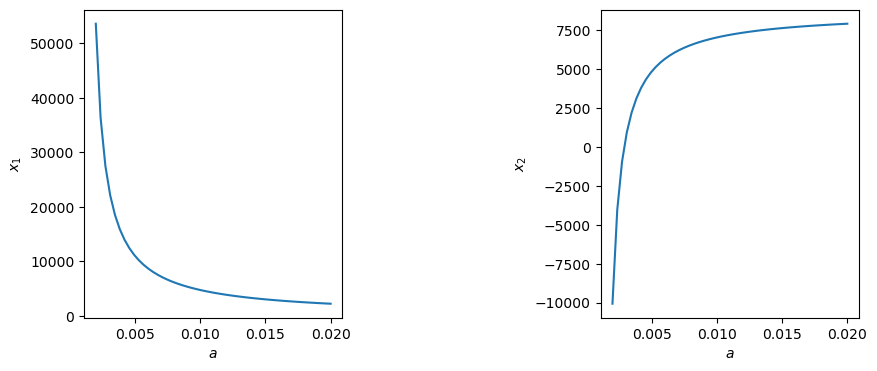
sp.var('a', pos=True)  #定义灵敏度分析的符号参数
y = (339-a*x1-0.003*x2)*x1+(399-0.004*x1-0.01*x2)*x2-(400000+195*x1+225*x2)
y = sp.simplify(y)   #化简
dy1 = y.diff(x1)     #求关于x1的偏导
dy2 = y.diff(x2)     #求关于x2的偏导
s = sp.solve([dy1, dy2], [x1, x2])
sx1 = s[x1]; sx2 = s[x2]  #提取解分量
s1 = sp.lambdify('a', sx1, 'numpy')  #符号函数转换为匿名函数
s2 = sp.lambdify('a', sx2, 'numpy')
a0 = plt.linspace(0.002, 0.02, 50)
plt.figure(figsize=(10, 4))
plt.subplots_adjust(wspace = 1)
plt.subplot(121); plt.plot(a0, s1(a0))
plt.xlabel('$a$'); plt.ylabel('$x_1$')
plt.subplot(122); plt.plot(a0, s2(a0))
plt.xlabel('$a$'); plt.ylabel('$x_2$')

dx1 = sx1.diff(a); dx10 = dx1.subs(a, 0.01)
sx1a = dx10 * 0.01 / 4735
dx2 = sx2.diff(a); dx20 = dx2.subs(a, 0.01)
sx2a = dx20 * 0.01 / 7043
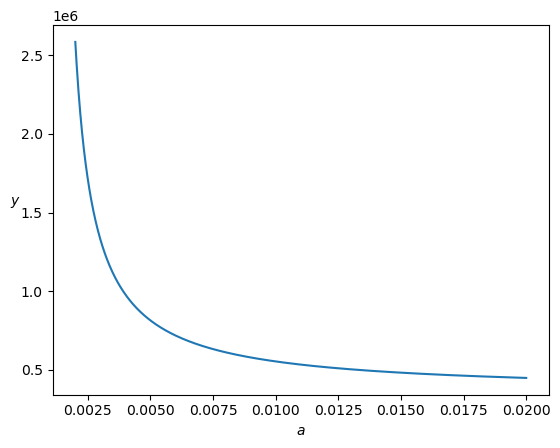
Y = y.subs({x1: s[x1], x2: s[x2]})  #求关于a的目标函数
Y = sp.factor(Y); Y = sp.simplify(Y)
Ya = sp.lambdify('a', Y, 'numpy')  #转换为匿名函数
a0 = plt.linspace(0.002, 0.02, 1000)
plt.figure(); plt.plot(a0, Ya(a0))
plt.xlabel('$a$'); plt.ylabel('$y$', rotation=0)
Sya = - 4735 ** 2 * 0.01 / 553641.025
y2 = y.subs({x1: 4735, x2: 7043, a: 0.011})  #计算近似最优利润
y3 = Y.subs(a, 0.011)   #计算最优利润
delta = (y3 - y2) / y2  #计算利润的相对误差
plt.show()

五、二次规划模型

例5.3 求解如下二次规划模型

max⁡f(x)=−x21−0.3x1x2−2x22+98x1+277x2s.t.{x1+x2≤100x1−2x2≤0x1,x2≥0\max f(x) = -x^1_2 - 0.3x_1x_2 - 2x^2_2 + 98x_1 + 277x_2 \\ s.t.\begin{cases} x_1 + x_2 \leq 100 \\ x_1 - 2x_2 \leq 0 \\ x_1, x_2 \geq 0 \end{cases}

# Lec0613_ex5_3
import cvxpy as cp
import numpy as np
c2 = np.array([[-1, -0.15],[-0.15, -2]])
c1 = np.array([98, 277])
a = np.array([[1, 1], [1, -2]])
b = np.array([100, 0])
x = cp.Variable(2, pos=True)
obj =cp.Maximize(cp.quad_form(x, c2) + c1 @ x)
con = [ a @ x <= b]
prob = cp.Problem(obj, con)
prob.solve(solver='CVXOPT')
print('最优解为：', np.round(x.value,4))
print('最优值为：', round(prob.value,4))

最优解为： [35.365 64.635]
最优值为： 11077.8703

例5.4（投资组合问题）

已知有A，B，C三种股票在过去12年的每年收益率如表5.2所列。请你从两个方面分别给出三支股票的投资比例：
（1）希望将投资组合中的股票收益的方差降到最小，以降低投资风险，并期望年收益率至少达到15%，那么应当如何投资？
（2）希望在方差最大不超过0.09的情况下，获得最大的收益。

表5.2 三种股票的年收益率数据

年份 A的收益率 B的收益率 C的收益率 年份 A的收益率 B的收益率 C的收益率
1 0.3 0.225 0.149 7 0.038 0.321 0.133
2 0.103 0.29 0.26 8 0.089 0.305 0.732
3 0.216 0.216 0.419 9 0.09 0.195 0.021
4 -0.056 -0.272 -0.078 10 0.083 0.39 0.131
5 -0.071 0.144 0.169 11 0.035 -0.072 0.006
6 0.056 0.107 -0.035 12 0.176 0.715 0.908 
# Lec0614 例5.4
import cvxpy as cp
import numpy as np

a = np.loadtxt('../Data/Lec06/data5_4.txt')
mu = a.mean(axis=0)   #计算年平均收益
F = np.cov(a.T)       #计算协方差矩阵
x = cp.Variable(3, pos=True)
ob1 = cp.Minimize(cp.quad_form(x,F))
con1 = [ mu @ x >= 0.15, sum(x) == 1 ]
prob1 = cp.Problem(ob1, con1)
prob1.solve(solver='CVXOPT')
print('最优值为：', round(prob1.value,4))
print('最优解为：', np.round(x.value,4))

ob2 = cp.Maximize(mu @ x)
con2 = [sum(x) == 1, cp.quad_form(x, F) <= 0.09]
prob2 = cp.Problem(ob2, con2)
prob2.solve(solver='CVXOPT')
print('最优值为：', round(prob2.value,4))
print('最优解为：', np.round(x.value,4))


最优值为： 0.0228
最优解为： [0.5269 0.3578 0.1153]
最优值为： 0.2334
最优解为： [0.     0.0562 0.9438]

六、非线性规划的求解及应用

例5.5 求解如下二次规划模型

max⁡f(x)=−x12−0.3x1x2−2x22+98x1+277x2s.t.{x1+x2≤100x1−2x2≤0x1,x2≥0\max f(x) = -x^2_1 - 0.3x_1x_2 - 2x^2_2 + 98x_1 + 277x_2 \\ s.t.\begin{cases} x_1 + x_2 \leq 100 \\ x_1 - 2x_2 \leq 0 \\ x_1, x_2 \geq 0 \end{cases}

由于上述二次规划的目标函数不是凸函数，不能使用cvxpy库进行求解。使用Python软件求得的最优解为：x1=0,x2=0x_1=0, x_2=0，目标函数的最优值为0。

# Lec0615 例5.5
import numpy as np
from scipy.optimize import minimize

c2 = np.array([[-1, -0.15],[-0.15, -2]])
c1 = np.array([98, 277])
a = np.array([[1, 1], [1, -2]])
b = np.array([100, 0])
obj = lambda x: x @ c2 @ x + c1 @ x
con ={'type': 'ineq', 'fun': lambda x: b-a@x}
bd = [(0, np.inf) for i in range(a.shape[1])]
res = minimize(obj, np.random.randn(2), constraints=con, bounds=bd)
print(res)  #输出解的信息

 message: Optimization terminated successfully
 success: True
  status: 0
     fun: 4.913178150378678e-07
       x: [ 5.575e-10  1.576e-09]
     nit: 3
     jac: [ 9.800e+01  2.770e+02]
    nfev: 6
    njev: 2

例5.6 求下列非线性规划

max⁡f(x)=x12+x22+x23+8s.t.{x12−x2+x32≥0x1+x22+x33≤20−x1−x22+2=0x2+2x32=3x1,x2,x3≥0\max f(x) = x^2_1 + x_2^2 + x^3_2 + 8 \\ s.t.\begin{cases} x_1^2 - x_2 + x_3^2 \geq 0 \\ x_1 + x_2^2 + x_3^3 \leq 20 \\ -x_1 - x_2^2 +2 = 0 \\ x_2 + 2x_3^2 = 3 \\ x_1, x_2, x_3 \geq 0 \end{cases}

# Lec0615 例5.6
import numpy as np
from scipy.optimize import minimize

obj=lambda x: sum(x**2)+8
def constr1(x):
    x1, x2, x3 = x
    return [x1**2-x2+x3**2,
            20-x1-x2**2-x3**2]
def constr2(x):
    x1, x2, x3 = x
    return [-x1-x2**2+2, x2+2*x3**2-3]
con1={'type': 'ineq', 'fun': constr1}
con2={'type': 'eq', 'fun': constr2}            
con=[con1, con2]  #构造全部约束条件
bd = [(0, np.inf) for i in range(3)]
res = minimize(obj, np.random.randn(3), constraints=con, bounds=bd)
print(res)  #输出解的信息

message: Optimization terminated successfully
 success: True
  status: 0
     fun: 10.651091840604659
       x: [ 5.522e-01  1.203e+00  9.478e-01]
     nit: 6
     jac: [ 1.104e+00  2.407e+00  1.896e+00]
    nfev: 24
    njev: 6

例5.7 求下列非线性规划问题

min⁡z=∣x1∣+2∣x2∣+3∣x3∣4∣x4∣s.t.{x1−x2−x3+x4=0x1−x2+x3−3x4=1x1−x2−2x3+3x+4=−12\min z = |x_1| + 2|x_2| + 3|x_3| 4|x_4| \\ s.t.\begin{cases} x_1 - x_2 - x_3 + x_4 = 0 \\ x_1 - x_2 + x_3 - 3x_4 =1 \\ x_1 - x_2 -2x_3 + 3x+4 = -\frac{1}{2} \end{cases}

# Lec0616 例5.7
import cvxpy as cp
import numpy as np

c = np.arange(1, 5)
a = np.array([[1,-1,-1,1], [1,-1,1,-3], [1,-1,-2,3]])
b = np.array([0, 1, -1/2])
x = cp.Variable(4)
obj = cp.Minimize(c @ cp.abs(x))
con = [a @ x == b]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print("最优值为:", prob.value)
print("最优解为：\n", x.value)

最优值为: 1.25
最优解为：
 [ 0.25  0.    0.   -0.25]

# Lec0616 例5.7-2
import cvxpy as cp
import numpy as np

c = np.arange(1,5)
a = np.array([[1,-1,-1,1],[1,-1,1,-3],[1,-1,-2,3]])
b = np.array([0,1,-1/2])
u = cp.Variable(4, pos=True)
v = cp.Variable(4, pos=True)
obj = cp.Minimize(c@(u+v))
con = [a@(u-v)==b]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print("最优值为:", prob.value)
print("最优解为：\n", u.value, '\n', v.value)
print("原问题的最优解为：\n", u.value-v.value)

最优值为: 1.25
最优解为：
 [0.25 0.   0.   0.  ] 
 [0.   0.   0.   0.25]
原问题的最优解为：
 [ 0.25  0.    0.   -0.25]

例5.8 供应与选址

建筑工地的位置（用平面坐标表示，距离单位：km）及水泥日用量（单位：t）由表5.4给出。拟建两个料场向各工地运送水泥，两个料场日储量各为20t,问料场建在何处，使总的吨公里数最小。

表5.4 建筑工地的位置及水泥日用量表

1 2 3 4 5 6
a/km 1.25 8.75 0.5 3.75 3 7.25
b/km 1.25 0.75 4.75 5 6.5 7.75
c/t 3 5 4 7 6 11 
# Lec0617 例5.8
import numpy as np
from scipy.optimize import minimize

d = np.loadtxt('../Data/Lec06/data5_8.txt')
a = d[0]; b = d[1]; c = d[2]
e = np.array([20, 20])

def obj(xyz):
    x = xyz[: 2]; y = xyz[2: 4]
    z = xyz [4:].reshape(6,2)
    obj =0
    for i in range(6):
        for j in range(2):
            obj = obj + z[i,j] * np.sqrt((x[j]-a[i])**2+(y[j]-b[i])**2)
    return obj

con = []
con.append({'type': 'eq', 'fun': lambda z: z[4:].reshape(6,2).sum(axis=1)-c})
con.append({'type': 'ineq', 'fun': lambda z: e-z[4:].reshape(6,2).sum(axis=0)})
bd = [(0, np.inf) for i in range(16)]  #决策向量的界限
res = minimize(obj, np.random.rand(16), constraints=con, bounds=bd)
print(res)  #输出解的信息
s=np.round(res.x, 4)     #提出最优解的取值
print('目标函数的最优值：', round(res.fun,4))
print('x的坐标为：', s[:2])
print('y的坐标为：', s[2:4])
print('料场到工地的运输量为：\n', s[4:].reshape(6,2).T)

 message: Optimization terminated successfully
 success: True
  status: 0
     fun: 71.93519914703985
       x: [ 3.265e+00  7.250e+00 ...  2.248e-11  1.100e+01]
     nit: 46
     jac: [-7.629e-05  5.769e-01 ...  4.735e+00  0.000e+00]
    nfev: 821
    njev: 46
目标函数的最优值： 71.9352
x的坐标为： [3.2653 7.25  ]
y的坐标为： [5.192 7.75 ]
料场到工地的运输量为：
 [[ 3.  0.  4.  7.  6.  0.]
 [ 0.  5.  0.  0.  0. 11.]]

七、多目标规划

例5.9 生产规划问题

某公司考虑生产两种光电太阳能电池：产品甲和产品乙。这种生产会引起空气放射性污染。因此，公司经理有两个目标：极大化利润与极小化总的放射性污染。已知在一个生产周期内，每单位产品的收益、放射性污染排放量、机器能力(小时)、装配能力（小时）和可用的原材料（单位）的限制如表5.6所示。假设市场需求无限制，两种产品的产量和至少为10，则公司该如何安排一个生产周期内的生产。

# Lec0618 例5.9
import numpy as np
import cvxpy as cp

c1 = np.array([-2, -3])
c2 = np.array([1, 2])
a = np.array([[0.5, 0.25], [0.2, 0.2], [1, 5], [-1, -1]])
b = np.array([8, 4, 72, -10])
x = cp.Variable(2, pos=True)
obj = cp.Minimize(0.5 * (c1 + c2) @ x)
con = [a @ x <= b]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print('最优解为：', x.value)
print('最优值为：', prob.value)

obj1 = cp.Minimize(c1 @ x)
prob1 = cp.Problem(obj1, con)
prob1.solve(solver='GLPK_MI')
v1 = prob1.value  #第一个目标函数的最优值
obj2 = cp.Minimize(c2 @ x)
prob2 = cp.Problem(obj2, con)
prob2.solve(solver='GLPK_MI')
v2 = prob2.value  #第二个目标函数的最优值
print('两个目标函数的最优值分别为：', v1, v2)
obj3 = cp.Minimize((c1@x-v1)**2+(c2@x-v2)**2)
prob3 = cp.Problem(obj3, con)
prob3.solve(solver='CVXOPT')
print('解法二的最优解：', x.value)

con.append( c1 @ x == v1)
prob4 = cp.Problem(obj2, con)
prob4.solve(solver='GLPK_MI')
x3 = x.value   #提出最优解的值
print('解法三的最优解：', x3)
print('利润：', -c1@x3); print('排放污染物：', c2@x3)

最优解为： [12.  8.]
最优值为： -10.0
两个目标函数的最优值分别为： -53.0 10.0
解法二的最优解： [13.3598425   5.28031523]
解法三的最优解： [ 7. 13.]
利润： 53.0
排放污染物： 33.0

八、飞行管理问题

（本题选自1995年全国大学生数学建模竞赛A题）

本案例的详细教案请访问 Project06飞行管理问题

【第06讲】数学规划模型 返回首页

一、线性规划模型

二、整数规划模型

三、投资的收益与风险

四、非线性规划

五、二次规划模型

六、非线性规划的求解及应用

七、多目标规划

八、飞行管理问题

≡